각종 데이터 분석 실기시험 대비에 도움이 되는 파이썬 문법을 모아보았다. 그 네 번째로 머신러닝을 다룬다.
※ 본 내용은 Load 함수 블럭에서 iris.csv 파일을 불러온 후에 진행한다.iris.csv 다운받기 [클릭]
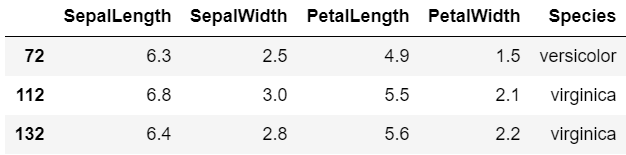
1 2 3 import pandas as pddf = pd.read_csv("iris.csv" ) df.head(2 )
데이터 세트 분할 Pandas 표본 추출 Pandas 데이터프레임의 .sample() 메서드의 인자는 다음과 같다.
- n: 표본 추출할 데이터(row) 개수frac: 표본 추출할 데이터(row) 비율replace: 복원추출 여부weights: 추출 데이터의 가중치(추출 대상 데이터의 row 개수와 여기에 입력되는 가중치 개수가 같아야 한다)random_state: 임의 확률과정 고정을 위한 자연수. np.random.seed() 기능과 같다.
1 2 df_sample = df.sample(n = 3 , random_state = 123 ) df_sample
train_test_split() 함수의 인자는 다음과 같다.
- arrays: 입력 데이터test_size: 평가 데이터의 비율 또는 개수(실수, 정수)train_size: 학습 데이터의 비율 또는 개수(실수, 정수)random_state: 임의 확률과정 고정을 위한 자연수. np.random.seed() 기능과 같다.suffle: 분리 전에 임의로 데이터를 섞는 기능stratify: 층화 표본 추출을 위한 인자
1 2 3 4 5 6 7 from sklearn.model_selection import train_test_splitdf_train, df_test = train_test_split(df, train_size = 10 ) len(df_train) len(df_test)
1 2 3 4 5 6 df_train, df_test = train_test_split(df, train_size = 0.7 ) len(df_train) len(df_test)
모델 성능 평가 수치형 종속변수 수치형 종속변수인 경우 오차 평가를 위해 다음의 객체를 준비한다.
1 2 3 4 5 from sklearn.metrics import mean_absolute_error from sklearn.metrics import mean_squared_error ser_true_value = pd.Series([1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ]) ser_pred_value = pd.Series([2 , 1 , 4 ,3 , 2 , 5 , 7 , 6 ])
- MSE: Mean Squared ErrorMAE: Mean Absolute ErrorRMSE: Root Mean Squared ErrorMAPE: Mean Absolute Percentage Errormean_absolute_percentage_error() 함수는 scikit-learn 0.24 버전 부터 사용 가능
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 print(mean_squared_error(y_true = ser_true_value, y_pred = ser_pred_value)) print(mean_squared_error(y_true = ser_true_value, y_pred = ser_pred_value) ** 0.5 ) print(mean_absolute_error(y_true = ser_true_value, y_pred = ser_pred_value)) print(abs((ser_true_value - ser_pred_value) / ser_true_value).sum() * 100 ) print(mean_absolute_percentage_error(y_true = ser_true_value, y_pred = ser_pred_value))
범주형 종속변수 범주형 종속변수인 경우 오분류 평가를 위해 다음의 객체를 준비한다.
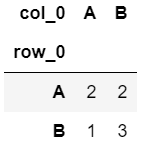
1 2 3 4 ser_true_class = pd.Series(["A" , "A" , "A" , "A" , "B" , "B" , "B" , "B" ]) ser_pred_class = pd.Series(["A" , "A" , "B" , "B" , "A" , "B" , "B" , "B" ]) pd.crosstab(ser_true_class, ser_pred_class)
오분류 평가를 위한 대표적인 개념은 다음과 같다.Accuracy: 정확도Precision: 정밀도(참이라고 분류한 것 중에서 실제 참인 것의 비율)Recall: 재현율(참인 것 중에서 참이라고 예측한 것의 비율)F1-score: 정밀도와 재현율의 조화평균
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 from sklearn.metrics import accuracy_scorefrom sklearn.metrics import precision_scorefrom sklearn.metrics import recall_scorefrom sklearn.metrics import f1_scoreprint(accuracy_score(y_true = ser_true_class, y_pred = ser_pred_class)) print(precision_score(y_true = ser_true_class, y_pred = ser_pred_class, pos_label = "A" )) print(recall_score(y_true = ser_true_class, y_pred = ser_pred_class, pos_label = "A" )) print(f1_score(y_true = ser_true_class, y_pred = ser_pred_class, pos_label = "A" ))
상기 코드에서 pos_label 의 pos 는 positive이며, 해당 인자에는 분류 정확도를 보고자 하는 목표값을 입력하면 된다.
선형회귀 선형회귀는 statsmodels 의 ols() 함수를 사용한 방법과 sklearn 의 LinearRegression() 함수를 사용한 방법이 있다. statsmodels 는 각종 통계량과 함께 상세한 선형회귀 결과를 확인할 수 있다.
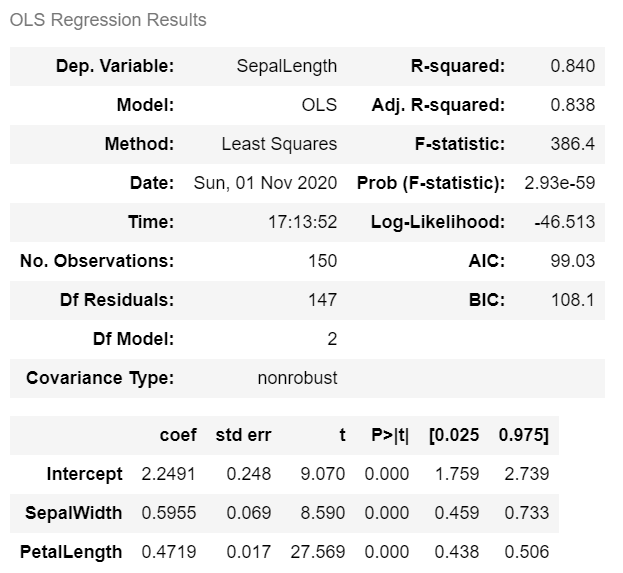
statsmodels 1 2 3 from statsmodels.formula.api import olsmodel_1 = ols("SepalLength ~ SepalWidth + PetalLength" , data = df).fit() model_1.summary()
sklearn sklearn 은 .summary() 메서드가 없고 상세 내역을 arribute를 사용하여 뽑아야 한다.
1 2 3 4 5 6 7 8 from sklearn.linear_model import LinearRegressionmodel_1 = LinearRegression(fit_intercept = True ) model_1.fit(X = df[["SepalWidth" , "PetalLength" ]], y = df["SepalLength" ]) model_1.coef_ model_1.intercept_
로지스틱회귀 분류 모델을 위해서 다음과 같이 Speciees 변수의 값을 활용하여 is_setosa 변수를 새로 만들어준다.
1 2 df["is_setosa" ] = (df["Species" ] == "setosa" ) + 0 df.head(2 )
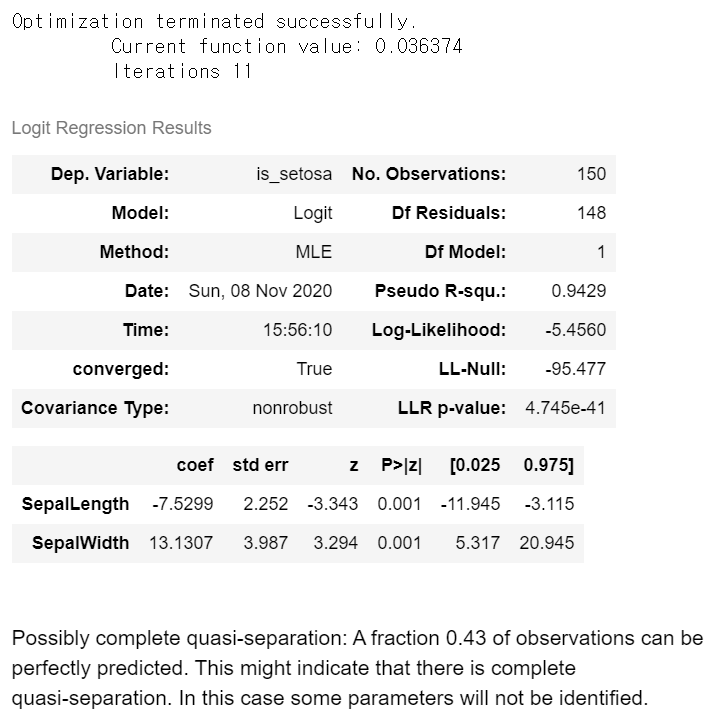
statsmodels 1 2 3 from statsmodels.api import Logitmodel_2 = Logit(endog = df["is_setosa" ], exog = df.iloc[:, :2 ]).fit() model_2.summary()
1 2 3 4 5 6 7 8 9 model_2.params np.exp(model_2.params)
sklearn 1 2 3 4 5 6 7 8 from sklearn.linear_model import LogisticRegressionmodel_2 = LogisticRegression(solver = "newton-cg" ).fit(X = df.iloc[:, :2 ], y = df["is_setosa" ]) model_2.coef_ np.exp(model_2.coef_)
k-means clustering 자격시험에서는 보통 결과를 고정하기 위해서 “random_state” attribute에 값을 할당하니 참고하도록 하자.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 from sklearn.cluster import KMeansmodel_3 = KMeans(n_clusters = 3 , random_state = 123 ).fit(X = df.iloc[:, :4 ]) model_3.cluster_centers_ model_3.labels_
군집 성능을 평가하기 위해서 사용하는 Silhouette score는 다음과 같이 산출한다.
1 2 3 from sklearn.metrics import silhouette_scoresilhouette_score(X = df_x, labels = model_3.labels_)
Hierarchical clustering 1 2 3 4 5 6 7 8 9 10 11 from sklearn.cluster import AgglomerativeClusteringmodel_4 = AgglomerativeClustering(n_clusters = 3 ).fit(X = df.iloc[:, :4 ]) model_4.labels_
k-NN 1 2 3 4 5 6 7 from sklearn.neighbors import KNeighborsClassifiermodel_5 = KNeighborsClassifier(n_neighbors = 5 ).fit(X = df.iloc[:, :4 ], y = df["Species" ]) model_5.predict(df.iloc[:, :4 ])[:20 ]
Decision Tree 1 2 3 4 5 6 7 8 9 10 11 from sklearn.tree import DecisionTreeClassifiermodel_6 = DecisionTreeClassifier().fit(X = df.iloc[:, :4 ], y = df["Species" ]) model_6.feature_importances_ model_6.predict(X = df.iloc[:, :4 ])[:20 ]
Naive Bayes 1 2 3 4 5 6 7 8 9 10 11 from sklearn.naive_bayes import GaussianNBmodel_7 = GaussianNB().fit(X = df.iloc[:, :4 ], y = df["Species" ]) model_7.classes_ model_7.predict_proba(df.iloc[:, :4 ])[:4 , ]
<실기시험 대비 시리즈 - Python>Python 실기시험 대비 정리 노트 - 00 Python 실기시험 대비 정리 노트 - 01 Python 실기시험 대비 정리 노트 - 02 Python 실기시험 대비 정리 노트 - 03 Python 실기시험 대비 정리 노트 - 04