Py) 실기시험 대비 정리 노트 - 03
Python / CheatSheet
11분 읽기 (대략 1676 단어)

Py) 실기시험 대비 정리 노트 - 03

각종 데이터 분석 실기시험 대비에 도움이 되는 파이썬 문법을 모아보았다. 그 세 번째로 통계를 다룬다.

상관분석

다양한 상관분석 기법이 있으나, 여기에서는 Pearson 상관분석과 순위 상관분석을 다룬다.

1
2
3
4
5
ser1 = pd.Series([1, 5, 2, 7, 10, 12])
ser2 = pd.Series([2, 3, 8, 9, 10, 15])

df_corr = pd.DataFrame([ser_1, ser_2]).transpose()
df_corr

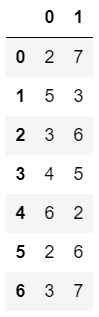
Pandas

Pandas는 DataFrame의 메서드로 .corr()을 제공한다. 별다른 옵션 없이 사용할 경우는 Pearson 상관계수를 계산한다. method 인자에는 다음과 같은 값을 입력할 수 있다.
- pearson : standard correlation coefficient
- kendall : Kendall Tau correlation coefficient
- spearman : Spearman rank correlation

1
df_corr.corr()

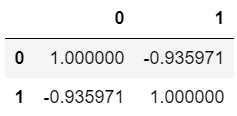
단, Pandas의 .corr() 메서드는 단순 상관계수만을 출력해주기 때문에 p-value 확인을 위해서는 SciPy 라이브러리를 활용해야 한다.

SciPy

SciPy의 함수는 상관계수 뿐만 아니라 p-value 또한 반환하기 때문에 보다 상세한 해석을 위해 사용한다. 결과는 검정통계량(왼쪽)과 p-value(오른쪽)가 tuple로 묶여서 출력된다.

1
2
3
4
5
6
7
8
9
10
11
12
from scipy.stats import pearsonr
from scipy.stats import spearmanr
from scipy.stats import kendalltau

pearsonr(ser1, ser2)
## (0.8257047804016666, 0.04292079349918977)

spearmanr(ser1, ser2)
## SpearmanrResult(correlation=0.942857142857143, pvalue=0.0048046647230320545)

kendalltau(ser1, ser2)
## KendalltauResult(correlation=0.8666666666666666, pvalue=0.016666666666666666)

독립성 검정

Pandas의 pd.crosstab() 으로 만든 결과물을 입력 하는 것을 추천한다.

1
2
3
4
5
6
7
8
9
10
11
df_chi2 = pd.DataFrame({"ID": ["A", "A", "A", "A", "A", "B", "B", "B", "B", "B"],
                        "YN": ["Y", "N", "N", "Y", "N", "Y", "Y", "N", "Y", "Y"]})

from scipy.stats import chi2_contingency
df_crosstab = pd.crosstab(df_chi2["ID"], df_chi2["YN"])
chi2_contingency(df_crosstab)
## (0.41666666666666663, # 검정통계량
##  0.5186050164287255,  # p-value
##  1,                   # 자유도
##  array([[2., 3.],     # 기대도수
##         [2., 3.]]))

위 결과는 p-value가 유의수준 5%(0.05) 기준으로 해당 값 보다 크기 때문에(0.5186) 귀무가설을 기각하지 못한다.


정규성 검정

정규성 검정은 종류가 제법 많지만 대표적으로 SciPy의 shapiro() 함수로 Shapiro-Wilk 검정을 실시할 수 있다.

1
2
3
4
5
ser_nor = pd.Series([4, 2, 5, 6, 7, 4, 5, 2, 6, 1, 3, 0, 15])

from scipy.stats import shapiro
shapiro(ser_nor)
## (0.8451932668685913, 0.024705516174435616)

위 결과는 p-value가 유의수준 5%(0.05) 기준으로 해당 값 보다 작기 때문에(0.024) 귀무가설을 기각하고 대립가설을 채택한다.

등분산 검정

1
2
ser_1 = pd.Series([2, 5, 3, 4, 6, 2, 3])
ser_2 = pd.Series([7, 3, 6, 5, 2, 6, 7])

Bartlett’s test

표본이 정규성을 따를 때 사용 가능한 등분산 검정법.

1
2
3
from scipy.stats import bartlett
bartlett(ser_1, ser_2)
## BartlettResult(statistic=0.3574441170696212, pvalue=0.549929145265077)

위 결과는 p-value가 유의수준 5%(0.05) 기준으로 해당 값 보다 크기 때문에(0.5499) 귀무가설을 기각하지 못한다.


Levene’s test

표본의 정규성 여부와 관계 없이 사용 가능한 등분산 검정법.

1
2
3
from scipy.stats import levene
levene(ser_1, ser_2)
## LeveneResult(statistic=0.1666666666666668, pvalue=0.6902818588864357)

위 결과는 p-value가 유의수준 5%(0.05) 기준으로 해당 값 보다 크기 때문에(0.6903) 귀무가설을 기각하지 못한다.



t-test

두 집단의 평균 차이를 검정하는 방법.
Scipy의 t-test 관련 함수는 공통적으로 결측치 처리 방법을 결정하는 nan_policy 인자가 있으나 되도록이면, 함수에 넣기 전에 결측치를 미리 처리하고 사용하는 것을 추천한다.

예제로 사용할 데이터는 다음과 같다.

1
2
ser_1 = pd.Series([2, 5, 3, 4, 6, 2, 3])
ser_2 = pd.Series([7, 3, 6, 5, 2, 6, 7])

단일 표본

SciPy의 ttest_1samp() 함수를 사용하며 표본집단을 Series로 넣고 모평균을 popmean 인자에 할당해준다.

1
2
3
from scipy.stats import ttest_1samp
ttest_1samp(ser_1, popmean = 5)
## Ttest_1sampResult(statistic=-2.499999999999999, pvalue=0.04652823228416732)

위 결과는 p-value가 유의수준 5%(0.05) 기준으로 해당 값 보다 작기 때문에(0.0465) 귀무가설을 기각하고 대립가설을 채택할 수 있다.


대응 표본

SciPy의 ttest_rel() 함수를 사용하며 각 표본집단을 Series로 넣어준다.

1
2
3
from scipy.stats import ttest_rel
ttest_rel(ser_1, ser_2)
## Ttest_relResult(statistic=-1.219715097075045, pvalue=0.2683379268893624)

위 결과는 p-value가 유의수준 5%(0.05) 기준으로 해당 값 보다 크기 때문에(0.2683) 귀무가설을 기각하지 못한다.


독립 표본

SciPy의 ttest_ind() 함수를 사용하며 각 표본집단을 Series로 넣어준다.
독립 2표본 t-test는 등분산 가정에 따라 equal_var 인자의 값을 다르게 준다.

1
2
3
4
5
6
from scipy.stats import ttest_ind
ttest_ind(ser_1, ser_2) # 1
## Ttest_indResult(statistic=-1.6840241981634352, pvalue=0.11798712107710582)

ttest_ind(ser_1, ser_2, equal_var = False) # 2
## Ttest_indResult(statistic=-1.684024198163435, pvalue=0.11958234592838302)

위 코드에서 1번 코드는 두 표본의 등분산, 2번 코드는 이분산으로 설정하고 계산하였다.
두 결과 모두 다 p-value가 유의수준 5%(0.05) 기준으로 해당 값 보다 크기 때문에 귀무가설을 기각하지 못한다.



One-way ANOVA

일원 분산분석은 SciPy와 StatsModels 라이브러리에서 각각 지원하며, 상세한 결과가 필요한 경우 StatsModels 라이브러리의 함수를 사용하는 것을 권장한다.

예제로 사용할 데이터는 다음과 같다.

1
2
3
4
5
6
ser_1 = pd.Series([2, 5, 3, 4, 6, 2, 3])
ser_2 = pd.Series([7, 3, 6, 5, 2, 6, 7])
ser_3 = pd.Series([9, 11, 4, 8, 2, 15, 3])

df_aov = pd.DataFrame([ser_1, ser_2, ser_3]).transpose().melt()
df_aov.head()

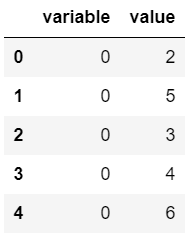
SciPy

- f_oneway(): Series 객체를 그룹별로 나눠서 입력
※ f_oneway(df[“group1”], df[“group2”], df[“group3”]) 

1
2
3
from scipy.stats import f_oneway
f_oneway(ser_1, ser_2, ser_3)
## F_onewayResult(statistic=2.783557046979866, pvalue=0.08844940319088185)

위 결과는 p-value가 유의수준 5%(0.05) 기준으로 해당 값 보다 크기 때문에(0.0884) 귀무가설을 기각하지 못한다.


StatsModels

StatsModels의 ols() 함수와 anova_lm() 함수를 불러와야 하기 때문에 SciPy의 함수보다 쓰기 번거롭다.

1
2
3
4
5
6
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm

formula = "value ~ C(variable)" # C() 범주형 변수임을 명시
lm = ols(formula, df_aov).fit()
anova_lm(lm)

위 결과는 p-value가 유의수준 5%(0.05) 기준으로 해당 값 보다 크기 때문에(0.0884) 귀무가설을 기각하지 못한다.


사후 검정

일원 분산분석에서 귀무가설을 기각하고 대립가설을 채택했을 때 어떤 집단간 평균이 유의미하게 차이가 나는지 확인하는 방법. 대표적으로 Tukey’s HSD가 있다.

1
2
3
4
5
6
7
8
9
10
from statsmodels.stats.multicomp import pairwise_tukeyhsd
print(pairwise_tukeyhsd(df_aov["value"], df_aov["variable"]))
## Multiple Comparison of Means - Tukey HSD, FWER=0.05
## ===================================================
## group1 group2 meandiff p-adj   lower  upper  reject
## ---------------------------------------------------
##      0      1   1.5714 0.6082 -2.6229 5.7658  False
##      0      2   3.8571 0.0746 -0.3372 8.0515  False
##      1      2   2.2857 0.3675 -1.9087 6.4801  False
## ---------------------------------------------------

위 결과의 경우 reject는 두 집단의 평균이 같다는 귀무가설을 기각하는지 여부를 알려준다. 즉, 모든 그룹간 평균이 유의미하게 다르다고 하기 어렵다(False).

<실기시험 대비 시리즈 - Python>
Python 실기시험 대비 정리 노트 - 00
Python 실기시험 대비 정리 노트 - 01
Python 실기시험 대비 정리 노트 - 02
Python 실기시험 대비 정리 노트 - 03
Python 실기시험 대비 정리 노트 - 04

# , , , , , ,
327142-eng.png
[R을 R려줘] R 데이터 시각화
326871-eng.png
[R을 R려줘] R 기초다지기

Inflearn에서 인강을 평생 소장하세요!

Py) 실기시험 대비 정리 노트 - 04
Py) 실기시험 대비 정리 노트 - 02

카테고리

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×