Py) 통계 - 기하 분포

개요

정의

베르누이 시행(Bernoulli Trial)에서 첫 번째 성공까지 시도한 횟수($X$)의 분포

실패를 기준으로 정의하는 기하 분포는 다음과 같다.

베르누이 시행(Bernoulli Trial)에서 첫 번째 성공까지 실패한 횟수($Y = X - 1$)의 분포

특징

기하 분포의 특징은 다음과 같다.

• 각 시행이 서로 독립
• 각 시행에서 성공 확률이 p로 일정
• 성공 횟수가 1회(첫 성공 후 시도가 중단됨)

기하 분포는 시도가 독립적이고, 각 시도에서의 ‘성공’ 확률이 일정하기 때문에 무기억성(Memoryless)의 특징이 있다. 즉, 과거의 시행에 영향을 받지 않는다.

응용

기하 분포는 다음과 같은 사례에 응용할 수 있다.

• (서비스 가입 이후)물건을 구입할 때 까지 필요한 로그인 횟수
• (앱 설치 후)앱을 삭제할 때 까지 걸린 일수

기타

기하 분포는 음이항 분포와 지수 분포와 관련이 있다.

음이항 분포는 “r번째 ‘성공’이 발생하기까지의 시도 횟수”와 관련된 분포인데 기하 분포는 음이항 분포에서 그 ‘성공’ 횟수가 1인 경우라고 할 수 있다.

지수 분포는 “연속 시간에서 첫 번째 ‘성공’이 일어나기까지의 시간”과 관련된 분포인데 기하 분포는 지수 분포에서 연속의 개념이 이산의 개념으로 된 것이라고 할 수 있다.

핵심 파라미터 및 관련 수식

파라미터

● $p$: 성공확률
● $k$: 첫 번째 ‘성공’이 발생하기까지의 시도 횟수

관련 수식

성공하기까지 시도한 횟수 $X$의 확률 질량 함수(probability mass function)는 다음과 같다.

기하 분포의 평균과 분산은 다음과 같다.

분포

확률을 0.2부터 1까지 변화시키면서 그린 기하 분포는 다음과 같다.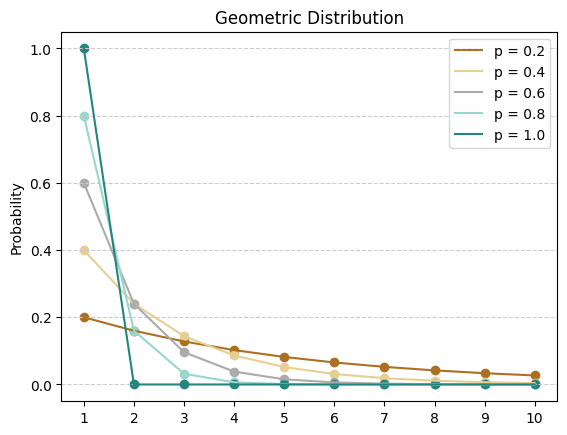

실습

기하 분포를 따르는 임의의 숫자를 생성하려면 다음과 같이 코드를 작성할 수 있다. rvs() 함수의 “p” 인자는 확률이고, “size”는 생성할 숫자의 개수이다.

1
2
3
4
5
6

import numpy as np
from scipy.stats import geom

np.random.seed(123)
geom.rvs(p = 0.2, size = 10)
## array([ 6,  2,  2,  4,  6,  3, 18,  6,  3,  3], dtype=int64)

이론 부분의 그래프를 그리기 위한 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

x = np.arange(1, 11)
p_values = np.linspace(0.2, 1, 5)

pal_brbg = sns.color_palette("BrBG", 5)
pal_brbg[2] = np.array(pal_brbg[2]) * 0.7

for idx, p in enumerate(p_values):
    y = (1 - p) ** (x - 1) * p
    plt.plot(x, y, color = pal_brbg[idx], label = f"p = {p:.1f}")
    plt.scatter(x, y, color = pal_brbg[idx])
    
plt.ylabel("Probability")
plt.title("Geometric Distribution")
plt.xticks(x)
plt.grid(axis = "y", linestyle = "--", color = "#CCCCCC")
plt.legend(loc = "upper right")
plt.show()