Py) 통계 - 기술통계(모양통계량)
Python / Stat
10분 읽기 (대략 1435 단어)

Py) 통계 - 기술통계(모양통계량)

파이썬으로 기술통계 중 모양 통계량의 계산에 대해 알아보자.

개요

기술 통계는 주어진 데이터 세트를 설명하고 요약하는 데 사용되는 통계 기법이며 다음과 같이 크게 세 종류로 나뉜다.

  1. 위치 통계량(Measures of Location)
  2. 변이 통계량(Measures of Dispersion)
  3. 모양 통계량(Measures of Shape)

이 중 모양 통계량에 대해 알아보고자 한다.

모양 통계량의 대표적인 통계량에는 왜도(skewness)와 첨도(kurtosis)가 있다. 이제 각 통계량을 알아보자.

왜도(skewness)

정의

왜도(歪度, skewness): 분포의 비대칭도를 측정하는 지표

수식

왜도($\gamma_1$)는 표준화된(standardized) 확률변수($X$)의 세제곱 평균(3차 적률)과 같다.

$$\gamma_1 := \tilde{\mu}_3 = E\left[\left(\frac{X - \mu}{\sigma}\right)^3\right]$$

특성

왜도 수치에 따른 특성은 다음과 같다.

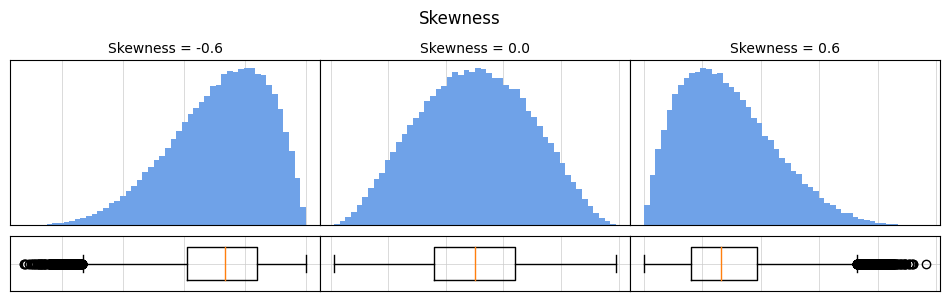
  • Skewness = 0: 데이터 분포가 대칭
  • Skewness > 0: 데이터 분포가 왼쪽(음수쪽)으로 치우쳐짐(right skewed, positively skewed, 오른쪽 꼬리가 긴 분포)
  • Skewness < 0: 데이터 분포가 오른쪽(양수쪽)으로 치우쳐짐(left skewed, negatively skewed, 왼쪽 꼬리가 긴 분포)

예제

다음의 예제를 통해 분포에 따른 왜도, 히스토그램, 상자수염 그림을 확인해보도록 하자. 여기서는 분포의 모양 뿐만 아니라 상자수염 그림의 상자 위치를 잘 보도록 한다.
왜도에 따른 분포

첨도(kurtosis)

정의

첨도(尖度, kurtosis): 분포의 중앙부분의 뾰족함 또는 꼬리부분의 길이에 대한 정보를 제공하는 통계량

수식

첨고($k$)는 표준화된(standardized) 확률변수($X$)의 네제곱 평균(4차 적률)과 같다.
$$k := \tilde{\mu}_4 = E\left[\left(\frac{X - \mu}{\sigma}\right)^4\right]$$

그런데 왜도처럼 기준을 0으로 잡기 위해 첨도에서 3을 뺀 초과 첨도(excess kurtosis)를 기준으로 계산하는 경우가 많다.
$$k_e := \tilde{\mu}_4 = E\left[\left(\frac{X - \mu}{\sigma}\right)^4\right] - 3$$

특성

일반적으로 말하는 첨도는 초과 첨도(excess kurtosis)이며 첨도 수치에 따른 특성은 다음과 같다.

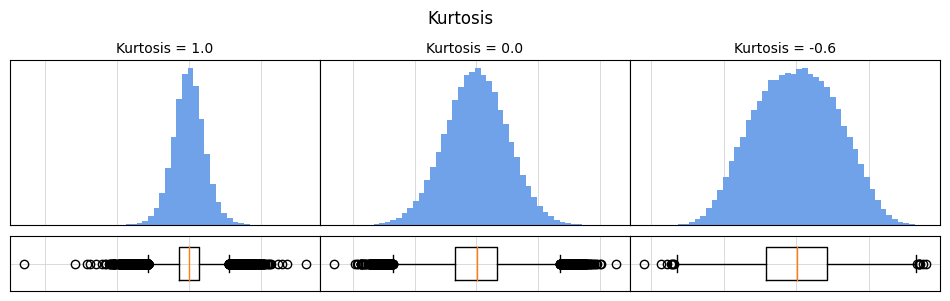
  • Kurtosis = 0(Mesokurtic): 정규분포와 같은 첨도
  • Kurtosis > 0(Leptokurtic): 꼬리가 두껍고 정규분포보다 뾰족한 분포
  • Kurtosis < 0(Platykurtic): 꼬리가 얇고 정규분포보다 완만한 분포

n개의 확률변수 $X_{1}, \dots, X_{n}$ 가 서로 독립이고 같은 분산일 경우 다음의 특성이 성립한다.
$$Kurt[X_1 + \dots + X_n ] = \frac{1}{n^2}(Kurt[X_1] + \dots + Kurt[X_n])$$

그리고 첨도가 정의될 수 있다면, 해당 값은 최소 1 이상이다.
※ 상한은 없음

$$Kurt[X] \ge 1$$

예제

다음의 예제를 통해 분포에 따른 첨도, 히스토그램, 상자수염 그림을 확인해보도록 하자. 여기서는 분포의 모양 뿐만 아니라 상자수염 그림의 상자 너비를 잘 보도록 한다.
첨도에 따른 분포

실습

NumPy

NumPy 라이브러리는 왜도와 첨도를 계산하기 위한 함수나 메서드를 지원하지 않는다.

Pandas

Pandas 라이브러리는 객체의 .skew()와 .kurt() 메서드가 각각 왜도와 첨도를 지원하며 첨도의 경우 .kurtosis() 메서드도 있으며 해당 메서드의 연산 결과는 .kurt()와 같다. 그리고 기본적으로 모집단에 대한 통계량(비편향, 표본이 아닌)을 계산한다.

1
2
3
4
5
6
7
8
9
import pandas as pd

ser = pd.Series([1, 5, 2, 7, 2, 3, 3, 10])

ser.skew()
## 1.1791140969556215

ser.kurt(), ser.kurtosis()
## (0.6866918373483912, 0.6866918373483912)

SciPy

SciPy 라이브러리는 skew()와 kurtosis() 함수가 각각 왜도와 첨도를 지원한다. 그리고 각 함수는 기본적으로 표본에 대한 통계량(편향, 모집단이 아닌)을 계산한다. 만약, 모집단에 대한 통계량을 산출하고자 한다면 bias = False를 추가하면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
from scipy.stats import skew
from scipy.stats import kurtosis

arr = np.array([1, 5, 2, 7, 2, 3, 3, 10])

skew(arr)
## 0.9453944937264186

kurtosis(arr)
## -0.3396705536436233

skew(arr, bias = False)
## 1.1791140969556215

kurtosis(arr, bias = False)
## 0.6866918373483912

그래프 - 왜도

이론부분의 왜도 그래프를 그리기 위한 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import skew

np.random.seed(123)
arr_1 = np.random.beta(a = 5, b = 2, size = 100000)
arr_2 = np.random.beta(a = 3, b = 3, size = 100000)
arr_3 = np.random.beta(a = 2, b = 5, size = 100000)

fig, axes = plt.subplots(nrows = 2, ncols = 3, figsize = (12, 3), 
                       gridspec_kw = {"height_ratios": [3, 1]})

for i, ax in enumerate(axes.ravel()):
    ax.grid(color = "#CCCCCC", linewidth = 0.5, zorder = 1)
    ax.tick_params(length = 0)
    ax.set_xticklabels([])
    ax.set_yticks([])

axes[0, 0].hist(arr_1, bins = 50, color = "#6FA2E8", zorder = 2)
axes[0, 0].set_title("Skewness = " + str(round(skew(arr_1), 1)), size = 10)
axes[1, 0].boxplot(arr_1, widths = 0.6, vert = False)
axes[0, 1].hist(arr_2, bins = 50, color = "#6FA2E8", zorder = 2)
axes[0, 1].set_title("Skewness = " + str(round(abs(skew(arr_2)), 1)), size = 10)
axes[1, 1].boxplot(arr_2, widths = 0.6, vert = False)
axes[0, 2].hist(arr_3, bins = 50, color = "#6FA2E8", zorder = 2)
axes[0, 2].set_title("Skewness = " + str(round(skew(arr_3), 1)), size = 10)
axes[1, 2].boxplot(arr_3, widths = 0.6, vert = False)

for n_col in range(3):
    axes[1, n_col].set_yticklabels([""])

plt.subplots_adjust(hspace = 0.1,  wspace = 0)
plt.suptitle("Skewness", size = 12, y = 1.05)
plt.show()

그래프 - 첨도

이론부분의 첨도 그래프를 그리기 위한 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, kurtosis

np.random.seed(123)
arr_1 = t.rvs(10, size = 100000)
arr_2 = np.random.normal(loc = 0, scale = 1, size = 100000)
arr_3 = t.rvs(30, size = 100000) + np.random.uniform(-10, 10, 100000) * 0.2 + np.random.uniform(-5, 5, 100000) * 0.8

fig, axes = plt.subplots(nrows = 2, ncols = 3, figsize = (12, 3), 
                         gridspec_kw = {"height_ratios": [3, 1]})

for i, ax in enumerate(axes.ravel()):
    ax.grid(color = "#CCCCCC", linewidth = 0.5, zorder = 1)
    ax.tick_params(length = 0)
    ax.set_xticklabels([])
    ax.set_yticks([])

axes[0, 0].hist(arr_1, bins = 50, color = "#6FA2E8", zorder = 2)
axes[0, 0].set_title("Kurtosis = " + str(round(kurtosis(arr_1), 1)), size = 10)
axes[1, 0].boxplot(arr_1, widths = 0.6, vert = False)
axes[0, 1].hist(arr_2, bins = 50, color = "#6FA2E8", zorder = 2)
axes[0, 1].set_title("Kurtosis = " + str(round(abs(kurtosis(arr_2)), 1)), size = 10)
axes[1, 1].boxplot(arr_2, widths = 0.6, vert = False)
axes[0, 2].hist(arr_3, bins = 50, color = "#6FA2E8", zorder = 2)
axes[0, 2].set_title("Kurtosis = " + str(round(kurtosis(arr_3), 1)), size = 10)
axes[1, 2].boxplot(arr_3, widths = 0.6, vert = False)

for n_col in range(3):
    axes[1, n_col].set_yticklabels([""])

plt.subplots_adjust(hspace = 0.1,  wspace = 0)
plt.suptitle("Kurtosis", size = 12, y = 1.05)
plt.show()
# , , , , , , , , , , , ,
327142-eng.png
[R을 R려줘] R 데이터 시각화
326871-eng.png
[R을 R려줘] R 기초다지기

Inflearn에서 인강을 평생 소장하세요!

Py) 통계 - 포아송 분포
Py) 통계 - 이항 분포

카테고리

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×