이산확률분포인 이항 분포(二項 分布, Binomial Distribution)에 대해 알아본다.
개요
정의
이항 분포(Binomial Distribution)는 베르누이 시행(Bernulli Trial)을 $n$번 반복했을 때의 “성공” 횟수를 나타내는 확률 분포
성공 확률이 $p$인 베르누이 시행을 $n$번 반복하여 관찰되는 성공 횟수를 $X$라고 할 때, $X$는 이항 분포를 따른다.
특징
● $X$는 0부터 $n$까지의 정수 값을 가짐
● 이항 분포의 평균은 $np$이며, 분산은 $np(1−p)$
● 이항 분포는 $n$번의 독립적인 베르누이 시행 결과에 대한 분포
● $n$이 매우 크고 $p$가 매우 작은 경우 $\lambda = np$인 포아송 분포에 근사
● $n$이 매우 크고 $p$가 매우 작거나 크지 않은 경우 계산의 편의를 위해 평균이 $np$이고 분산($\sigma^2$)이 $np(1-p)$인 정규분포로 간주할 수 있음
※ 근사시 연속성 수정(continuity correction) 고려 가능
핵심 파라미터 및 관련 수식
파라미터
● $n$: 시행횟수
● $p$: 확률
관련 수식
이산 확률 변수 $X$에 대한 확률질량함수(probability mass function)는 다음과 같다.
$$P(X = k) = \begin{pmatrix} n \\ k \end{pmatrix} p^{k}(1-p)^{n-k} = \frac{n!}{k!(n-k)!} p^{k}(1-p)^{n-k}$$
분포
이항 분포를 따르는 임의의 숫자 1000개를 시각화 하면 다음과 같다.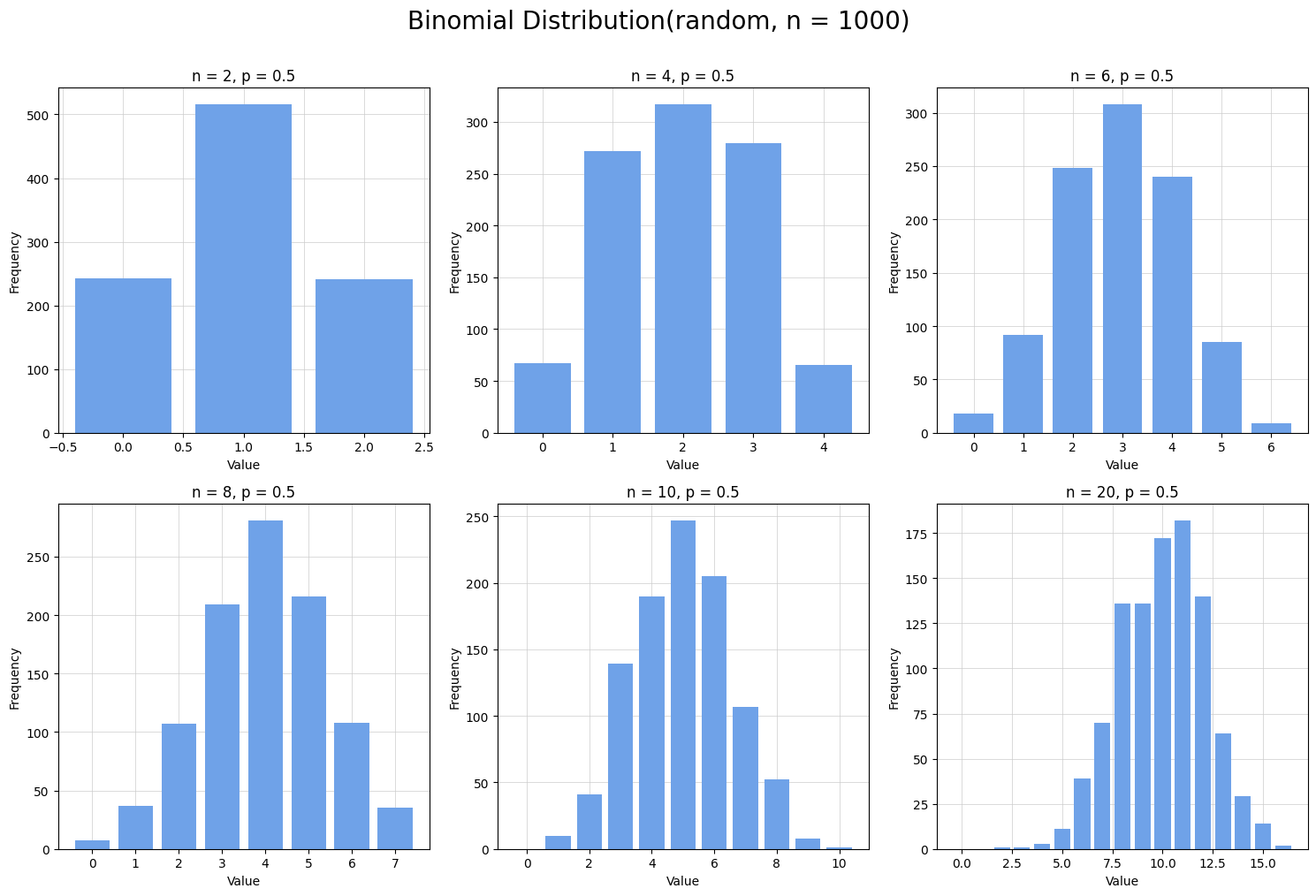
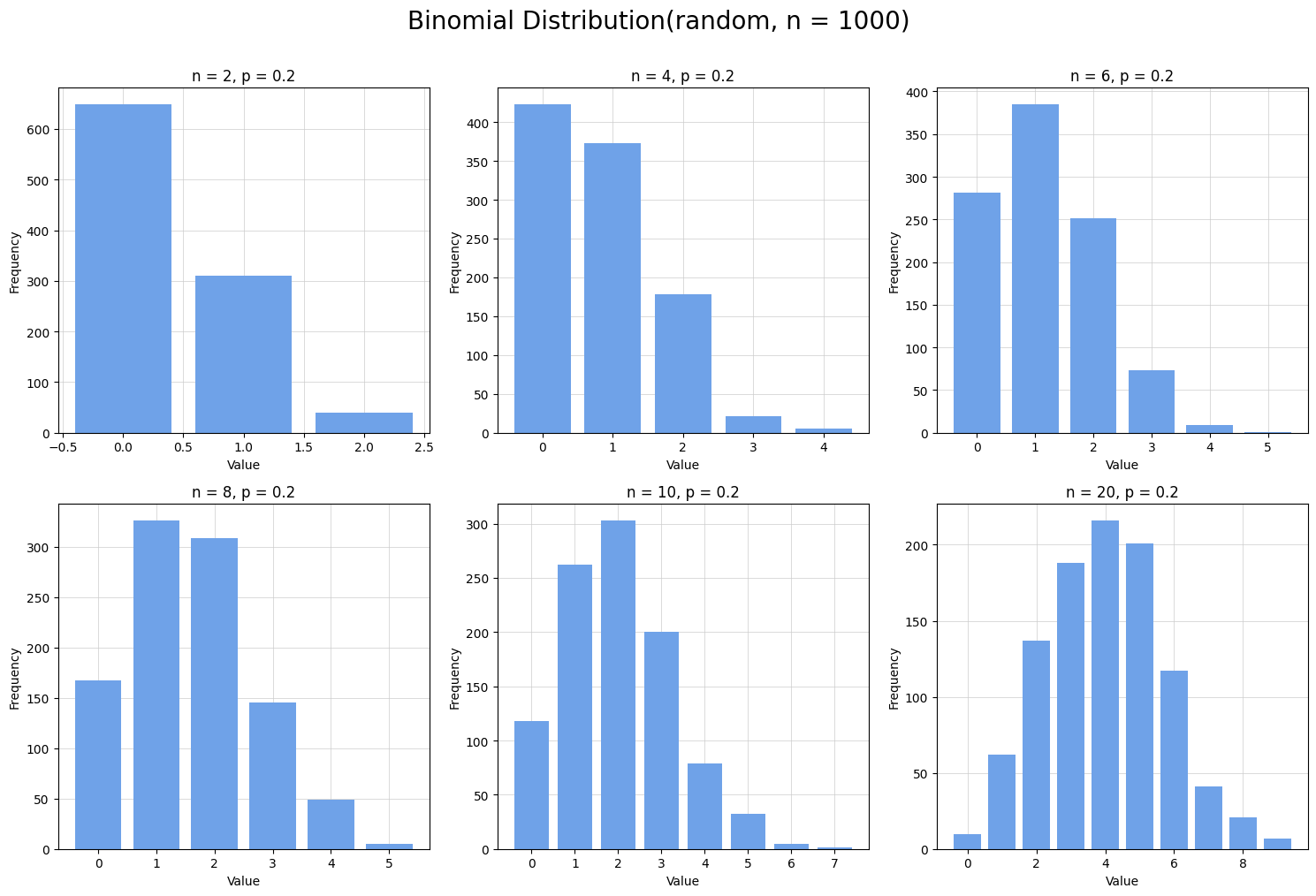
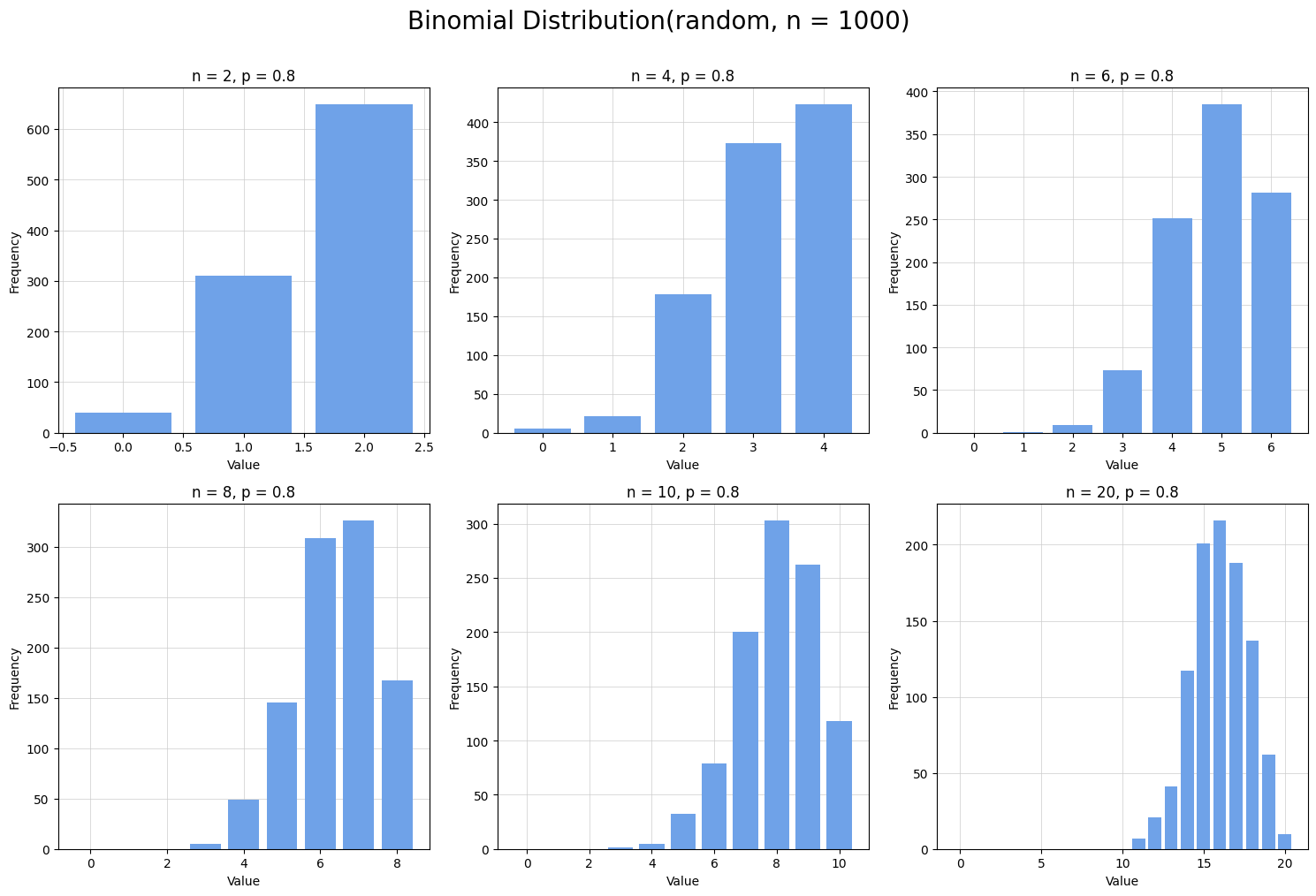
기타
로지스틱 회귀분석과 관련이 있다.
실습
베르누이 분포를 따르는 임의의 숫자를 생성하려면 다음과 같이 코드를 작성할 수 있다.
1 | from scipy.stats import binom |
이론 부분의 분포를 그리기 위해 사용된 코드는 다음과 같다.
1 | np.random.seed(123) |
