브라이틱스(Brightics)에서 독립 2 표본 t-검정을 실시할 수 있는 함수 블럭인 Two Sample T Test For Stacked Data를 알아본다.
Statistics
※ 본 내용은 Load 함수 블럭에서 bike.csv 파일을 불러온 후에 진행한다.
※ bike.csv 다운받기 [클릭]
개요
t-검정은 두 집단 간의 평균을 비교하는 모수적 통계기법으로 표본이 오차항의 정규성, 등분산성, 독립성을 만족할 경우 사용이 가능하며 모분산을 알 경우는 z-검정을 실시할 수 있다. t-검정은 세 종류의 검정이 있는데 단일 표본(One Sample), 대응 표본(Paired Sample), 독립 2 표본(Independent 2 Sample) 이다. 그 중 세 번째인 독립 2 표본 t-검정을 알아본다.
※ 단일 표본 t-검정 포스팅 바로가기 -> [클릭]
※ 대응 표본 t-검정 포스팅 바로가기 -> [클릭]
독립 2 표본 t-검정에서 필요한 것은 독립인 두 표본 집단이다. 가끔 t-test가 평균 비교라고 해서 표본자료의 평균값을 미리 구해서 그 값을 검정에 사용하는 경우가 있는데 잘 확인해야 한다. 표본의 평균은 검정통계량 t를 계산할 때 활용되니 Two Sample T Test For Stacked Data 블럭을 사용할 때는 계산된 평균값이 아닌 원 자료를 입력하도록 하자. 그리고 Paired T Test 블럭과 Two Sample T Test for Stacked Data 블럭은 입력하는 자료구조가 서로 다르니 주의해야 한다.
다른 t-검정과 다른 점은 표본 자료가 등분산여부에 따라 검정통계량 계산 식이 달라지기 때문에 확인하고 구분하여 분석을 실시해야 한다. 등분산 검정은 Bartlett's Test 블럭으로 확인할 수 있다. 그리고 이분산일 경우 Welch’s t-검정도 사용이 가능하다.
※ Bartlett 검정 포스팅 바로가기 -> [클릭]
단, 표본의 오차항이 정규성을 만족하지 못하는 경우 맨-휘트니 검정(Mann-Whinety Test)을 사용해야 한다.
통계량 계산
검정통계량 t는 등분산의 경우 다음과 같이 계산한다.
검정통계량 t는 이분산의 경우 다음과 같이 계산한다.
가설
- 귀무가설($𝐻_0$): 두 표본의 평균은 같다.
- 대립가설($𝐻_1$): 두 표본의 평균은 다르다.
설정
Two Sample T Test For Stacked Data 블럭의 설정 창은 다음과 같다.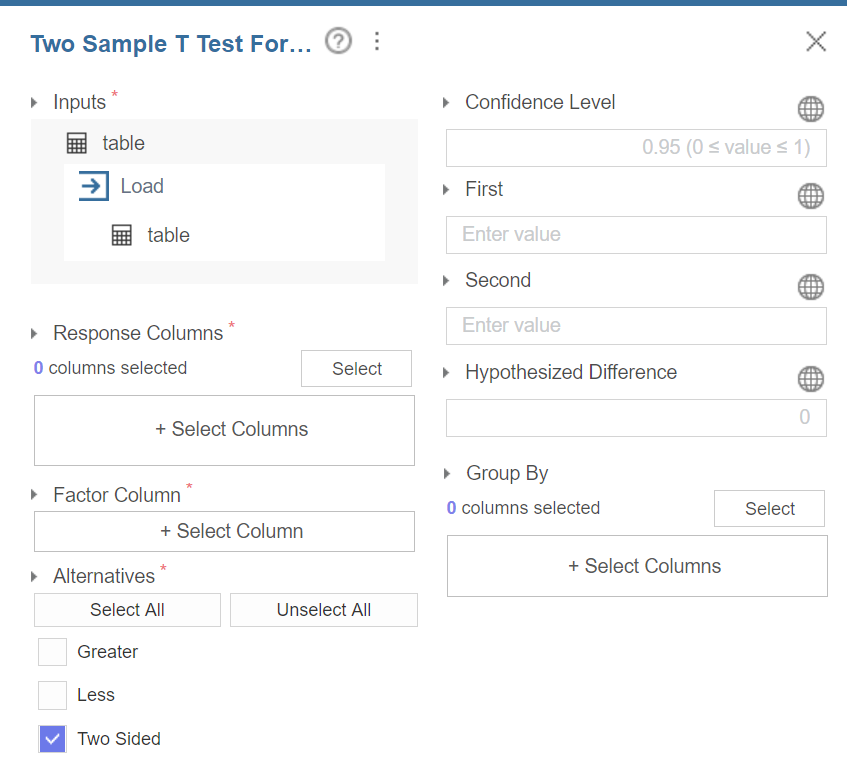
Response Column 과 Factor Column 에는 각각 독립 2 표본 t-검정을 실시할 변수를 지정해준다. 전자에는 수치형 자료가 위치해야 하고 후자에는 해당 수치형 변수를 구분하는 범주형 자료가 위치해야하니 주의하자.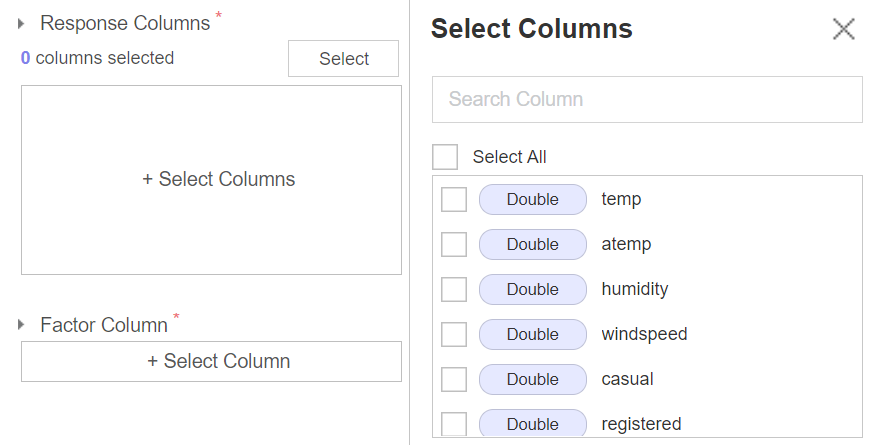
Alternatives 에는 “Greater”, “Less”, “Two Sided” 세 개의 선택지가 있는데 이는 단측검정과 양측검정의 결과를 별도로 보고자 할 때 원하는 것을 선택한다. 예를 들어 두 표본 의 평균이 0 보다 큰지 그렇지 않은지 검정하고 싶다면 “Greater”를, 두 표본의 평균이 0보다 작은지 그렇지 않은지 검정하고 싶다면 “Less”를, 두 표본의 평균이 0과 차이가 나는지 그렇지 않은지 검정하고 싶다면 “Two Sided”를 선택하면 된다.
Hypothesized Difference 는 두 집단의 평균이 같지 않고 특정한 값 만큼 차이가 난다는 가정을 하고자 할 때 여기에 해당 값을 입력한다. 예를 들어 전년도 대비 올해의 방문하는 손님 수가 일평균 50명이 증가했다고 할 때 정말 50명이 증가했는지 그렇지 않은지 확인하고싶다면 여기에 50을 입력하면 된다.
Confidence Level 신뢰수준을 의미한다. 기본값으로 95가 입력되어있는데 이는 95% 신뢰구간, 5% 유의수준을 의미한다. 이 값을 조정하면 산출되는 신뢰구간(confidence interval)의 값이 바뀌는 것을 볼 수 있다.
추가로 특정 변수의 원소를 기준으로 묶음 연산을 하고자 할 때는 대상이 되는 변수를 아래 Group By 부분에서 [Select] 버튼을 눌러 변수 목록을 불러와 선택해준다. 묶음 연산은 되도록이면 연속형 변수가 아닌 명목형 변수를 기준으로 수행을 권장한다.
결과
다음 결과는 정기권 이용자의 자전거 대여 수 인 registered 변수를 종속변수로 하고 공휴일 여부인 holiday 변수를 독립변수로 한 결과이다. 추가로 이분산 가정으로 실시한 결과이다.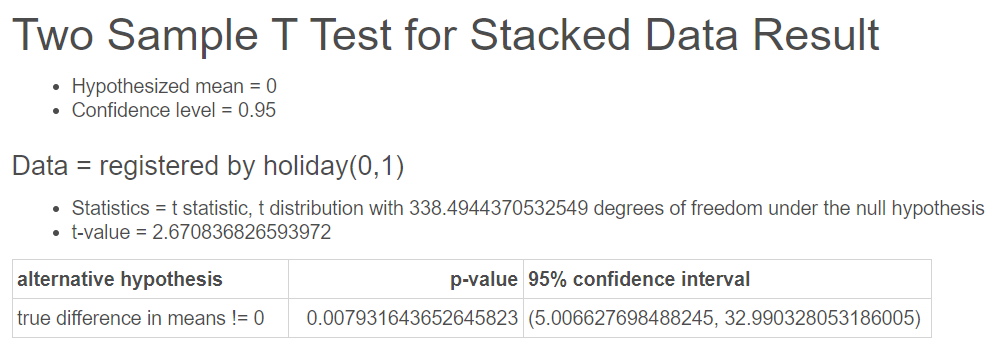
검정통계량 t는 2.671이고 p-value는 0.008 이다. 즉, 유의수준 5%(0.05) 기준으로 p-value가 0.008로 유의수준 보다 작기 때문에 귀무가설을 기각하고 대립가설을 채택하여 두 표본의 평균은 같지 않고 유의하게 차이가 난다고 할 수 있다.


