브라이틱스(Brightics)에서 단일 표본 t-검정을 실시할 수 있는 함수 블럭인 One Sample T Test를 알아본다.
Statistics
※ 본 내용은 Load 함수 블럭에서 bike.csv 파일을 불러온 후에 진행한다.
※ bike.csv 다운받기 [클릭]
개요
t-검정은 두 집단 간의 평균을 비교하는 모수적 통계기법으로 표본이 오차항의 정규성, 등분산성, 독립성을 만족할 경우 사용이 가능하며 모분산을 알 경우는 z-검정을 실시할 수 있다. t-검정은 세 종류의 검정이 있는데 단일 표본(One Sample), 대응 표본(Paired Sample), 독립 2 표본(Independent 2 Sample) 이다. 그 중 첫 번째인 단일 표본 t-검정을 알아본다.
※ 대응 표본 t-검정 포스팅 바로가기 -> [클릭]
※ 독립 2 표본 t-검정 포스팅 바로가기 -> [클릭]
단일 표본 t-검정에서 필요한 것은 단일 표본 자료와 모평균이다. 가끔 t-test가 평균 비교라고 해서 표본자료의 평균값을 미리 구해서 그 값을 검정에 사용하는 경우가 있는데 잘 확인해야 한다. 표본의 평균은 검정통계량 t를 계산할 때 활용되니 One Sample T Test 블럭을 사용할 때는 계산된 평균값이 아닌 원 자료를 입력하도록 하자.
단, 표본의 오차항이 정규성을 만족하지 못하면서 표본이 대칭분포를 따르지 않는 경우 단일 표본 부호 검정(1 Sample Wilcoxon Signed Rank Test)을 사용해야 하고 표본의 오차항이 정규성을 만족하지 못하면서 표본이 대칭분포를 따르는 경우 단일 표본 윌콕슨 부호순위 검정(Wilcoxon )
통계량 계산
검정통계량 t는 다음과 같이 계산한다.
가설
- 귀무가설($𝐻_0$): 표본 평균과 모평균이 같다.
- 대립가설($𝐻_1$): 표본 평균과 모평균이 다르다.
설정
One Sample T Test 블럭의 설정 창은 다음과 같다.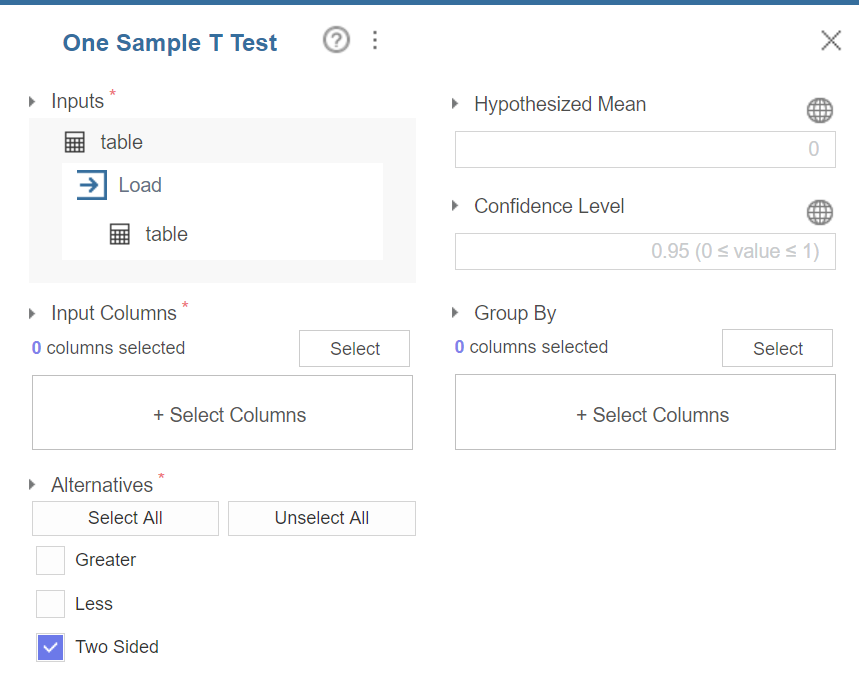
Input Columns 에는 t-검정을 실시할 변수를 지정해준다.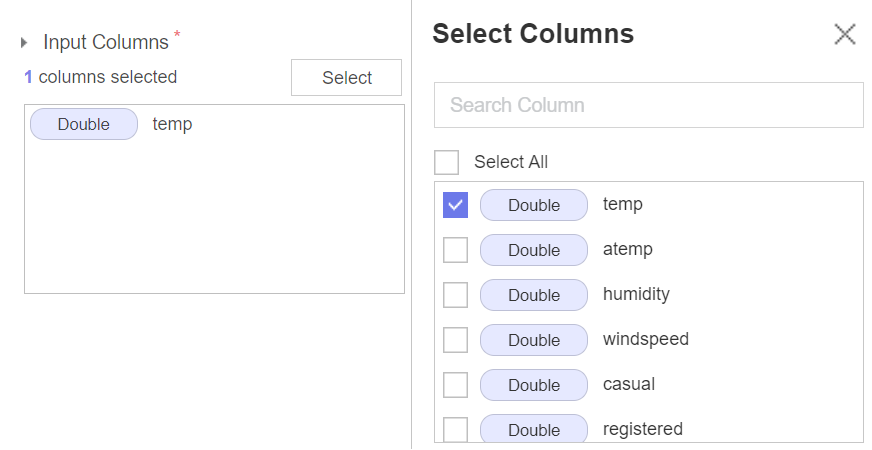
Alternatives 에는 “Greater”, “Less”, “Two Sided” 세 개의 선택지가 있는데 이는 단측검정과 양측검정의 결과를 별도로 보고자 할 때 원하는 것을 선택한다. 예를 들어 표본 평균이 모평균 보다 큰지 그렇지 않은지 검정하고 싶다면 “Greater”를, 표본 평균이 모평균 보다 작은지 그렇지 않은지 검정하고 싶다면 “Less”를, 표본 평균이 모평균과 차이가 나는지 그렇지 않은지 검정하고 싶다면 “Two Sided”를 선택하면 된다.
Hypothesized Mean 에는 모평균을 입력한다. 기본값은 0으로 되어있는데 변경이 필요할 경우 직접 그 숫자를 기입하면 된다.
Confidence Level 신뢰수준을 의미한다. 기본값으로 95가 입력되어있는데 이는 95% 신뢰구간, 5% 유의수준을 의미한다. 이 값을 조정하면 산출되는 신뢰구간(confidence interval)의 값이 바뀌는 것을 볼 수 있다.
추가로 특정 변수의 원소를 기준으로 묶음 연산을 하고자 할 때는 대상이 되는 변수를 아래 Group By 부분에서 [Select] 버튼을 눌러 변수 목록을 불러와 선택해준다. 묶음 연산은 되도록이면 연속형 변수가 아닌 명목형 변수를 기준으로 수행을 권장한다.
결과
기온 정보가 들어있는 temp 변수의 평균과 모평균 20을 양측검정(Two Sided)으로 비교했을 때의 결과는 다음과 같다.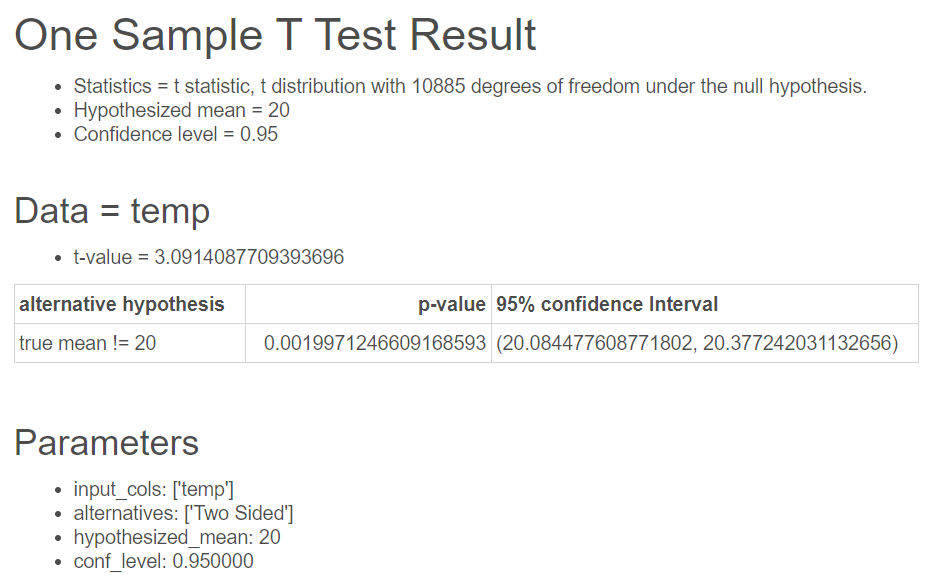
검정통계량 t는 3.091이고 p-value는 0.002 이다. 즉, 유의수준 5%(0.05) 기준으로 p-value가 0.002로 유의수준 보다 작기 때문에 귀무가설을 기각하고 대립가설을 채택하여 표본 평균과 모평균은 유의하게 차이가 난다고 할 수 있다.


