브라이틱스(Brightics)에서 다중 집단의 등분산 검정이 가능한 Levene's Test를 알아본다.
Statistics
※ 본 내용은 Load 함수 블럭에서 bike.csv 파일을 불러온 후에 진행한다.
※ bike.csv 다운받기 [클릭]
개요
등분산 검정중 하나인 Levene 검정은 집단간 분산이 같은지 다른지 여부를 알아볼 때 사용하기도 하고 독립 2표본 t-검정 또는 일원분산분석(one-way ANOVA) 실시 전에 가정 때문에 확인하는 용도로 사용하기도 한다. 그리고 Levene 검정은 두 집단 뿐만 아니라 세 집단 이상에서도 사용할 수 있으며 Bartlett 검정과 달리 표본이 정규성을 보이지 않아도 사용할 수 있다.
집단의 분포 특성에 따라 대표값을 평균, 중앙값, 절사평균값 셋 중에 하나로 설정하여 검정을 실시한다. 평균을 대표값으로 사용하는 경우는 정규분포처럼 표본 분포가 좌우 대칭(symmetric)이고 한쪽으로 치우친 분포가 아닐때(moderate-tail) 사용하고, 중앙값을 대표값으로 사용하는 경우는 카이제곱분포처럼 표본 분포가 한쪽으로 치우쳐져 있을 때 사용하고, 절사평균을 대표값으로 사용하는 경우는 표본 분포가 코시 분포(Cauchy distribution)와 같이 꼬리가 두꺼운 경우에 사용한다.
검정 통계량 계산
검정통계량 $W$는 다음과 같이 계산한다.
단, 여기서 $Z_ij$는 집단의 분포 특성에 기반하여 선택하는 대표값에 따라 계산 식이 달라진다.
가설
- 귀무가설($H_0$): 집단간 분산이 같다.
- 대립가설($H_1$): 적어도 두 집단간 분산이 다르다.
설정
Levene's Test 블럭의 설정 창은 다음과 같다.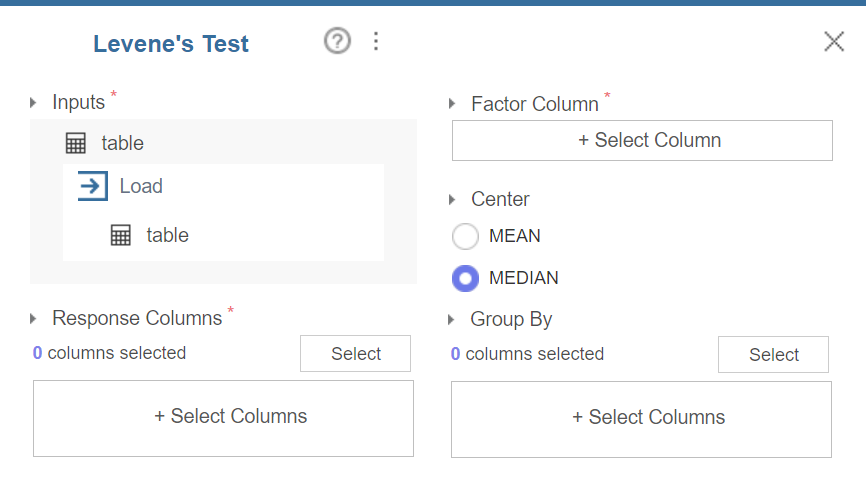
Center 에는 집단의 대표값을 설정하며 해당 설정과 그 설명은 다음과 같다.
- MEAN: Classical Levene’s Test 방법으로 평균을 기준으로 검정
- MEDIAN: Robust Brown-Forsythe 방법으로 중앙값을 기준으로 검정
※ 분포의 평균값이 대표값이라고 판단하기 어려운 경우
- TRIMMED: Levene-type Test 방법으로 절사평균(trimmed mean)을 기준으로 검정
※ 상, 하위 극단치 제거가 필요한 경우
결과
일일권으로 대여한 자전거 대여수를 의미하는 casual 변수를 종속변수로 하고 분기를 구분하는 season 변수를 독립변수로 하여 분기별 일일권 자전거 대여수의 분산이 같은지 다른지 검정한 결과는 다음과 같다.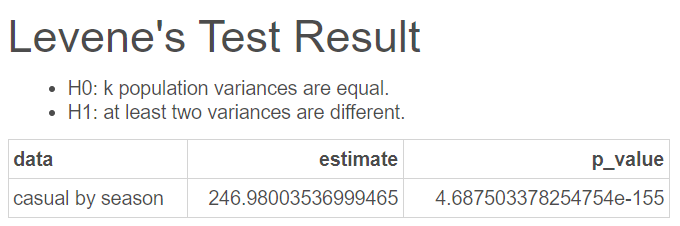
결과 중 estimate 는 검정통계량이고 p_value 는 p-value인데 이때 p-value가 4.688e-155로 유의수준 $\alpha$가 5%(0.05)일 때, p-value가 유의수준보다 작기 때문에 귀무가설을 기각하고 대립가설을 채택하여 적어도 두 집단간 분산이 다르다고 할 수 있다.


