Py) 통계 - 대응표본 t-검정

※ 본 내용에서 사용하는 data_for_ttest_rel.csv 파일은 별도로 다운로드 받아야 한다.
※ data_for_ttest_rel.csv 다운받기 [클릭]

이론

본 내용은 세 종류의 t-검정 중 두 번째인 대응표본 t-검정에 대해 다루며 t-검정의 목록은 다음과 같다.

1. 단일표본 t-검정
2. 대응표본 t-검정
3. 독립표본 t-검정

개요

대응표본 t-검정은 영문으로 Paired t-test 라고도 하는데 이 대응이라는 말은 두 집단이 서로 대응이 되며 짝이 된다는 것이다. 특히 이 검정은 의료통계에서 많이 사용되곤 하는데 예를 들어 약을 복용하기 전과 후의 혈압을 측정하여 약이 혈압에 영향을 미쳤는지를 검정할 때 사용된다. 이 때 약을 복용하기 전과 후의 혈압은 서로 대응이 되는 짝이 된다. 그래서 또 다른 표현으로 (의료)처치 전과 (의료)처치 후의 차이를 검정한다고도 한다.

추가로 예를 들자면 어떤 영양제의 효능을 실험하기 위해서 영양제를 섭취하기 전에 100m 전력질주를 하고 심박수가 일정 이하로 떨어지는 시간과 영양제를 섭취하고 난 후에 100m 전력질주를 하고 심박수가 일정 이하로 떨어지는 시간의 차이의 평균이 0과 유의미하게 다른지 알아보기 위해서도 이런 대응표본 t-검정을 사용할 수 있겠다.
※ 물론 이런 실험 설계는 통제변인과 조작변인을 잘 설정하여 진행해야 하겠다.

그리고 다음과 같이 어떤 사람의 10년 전의 IQ 또는 어떠한 신체적 수치와 현재 그 사람의 IQ 또는 어떠한 신체 수치를 통계적으로 비교하고 검정하기 위해 사용할 수도 있다.

상기 내용과 관련해서 데이터를 시각화 하면 다음과 같다.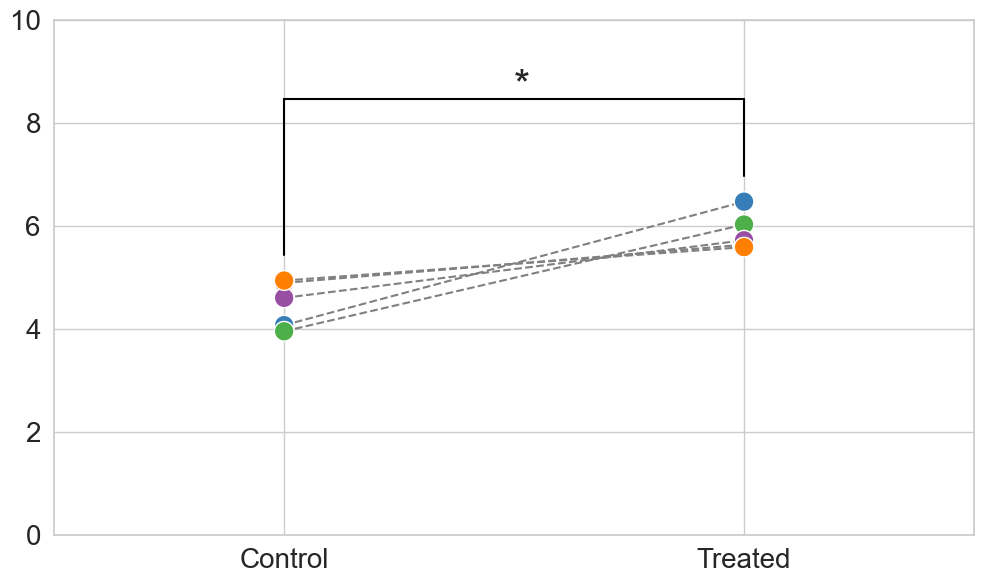

가설설정

짝이되는 두 데이터의 차이값의 평균이 0(또는 특정 값)과 다른지 비교하는 것이 좀 더 정확한 대응표본 t-검정의 핵심이 되겠다. 이 부분에서 많이들 어려움을 느끼는데 아래에서 “쌍의 의존성”에 대해 언급을 하지만, 일단 그림과 수식으로 설명하자면 다음과 같다.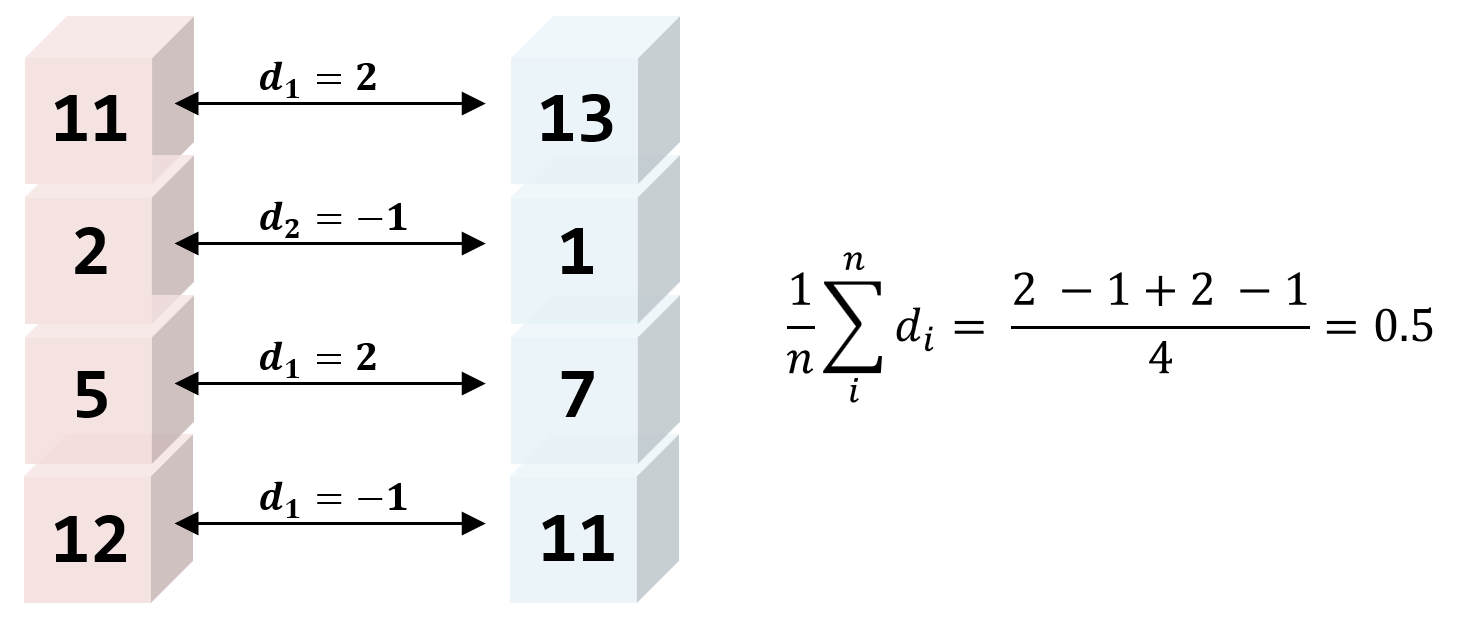

상기의 그림 처럼 각각의 짝이 되는 두 값의 차이($d_i$)를 산출하고 해당 값의 평균을 산출하게 되는데 이 값이 0(또는 특정 값)과 유의미하게 다른지 통계적으로 검정하는 것이 되겠다.

대응표본 t-검정의 원리와 검정통계량 산출식을 기반으로 귀무가설과 대립가설을 기술하자면 다음과 같다.

● 귀무가설($H_0$) : 짝이 되는 두 값의 차이의 평균이 0이나 다름 없다.
● 대립가설($H_1$) : 짝이 되는 두 값의 차이의 평균이 0이라고 보기 어렵다.

상기 내용을 좀 더 의역하자면 다음과 같다.

● 귀무가설($H_0$) : 두 집단의 평균은 같다.
● 대립가설($H_1$) : 두 집단의 평균은 같지 않다. (같다고 보기 어렵다.)

각 가설을 수식으로 표현하면 다음과 같다.

검정통계량

대응표본 t-검정의 검정통계량 t는 다음과 같이 계산할 수 있다.

여기서 $\bar{X}_d$는 쌍이 되는 표본 차이의 평균. 즉, 각 쌍의 측정값 간 차이의 평균, $\sigma_d$ 는 표본 차이의 표준편차, $n$은 표본의 크기이다.

가정

대응표본 t-검정의 가정은 다음과 같다.

• 정규성(Normality): $\bar{X}$는 평균이 $\mu$이고 분산이 $\sigma^2/n$인 정규분포를 따름
• 독립성(Independence): 표본의 관측값은 서로 독립이다. 즉, 표본의 관측값은 서로 영향을 주지 않음
• 쌍의 의존성(Paired Observations): 각 쌍의 관측값이 연관되어 있어야 함

쌍의 의존성과 관련해서는 비교 및 측정을 하기 위한 대상이 서로 매우 깊은 연관이 있거나 같은 대상에 대해 두 번의 측정이 이루어진 것을 말한다. 예를 들어 어떤 사람의 10년 전의 IQ 또는 어떠한 신체적 수치와 현재 그 사람의 IQ 또는 어떠한 신체 수치를 통계적으로 비교하고 검정하기 위해 사용할 수 있다. 이런 경우에는 쌍의 의존성이 있다고 볼 수 있다.

실습

라이브러리 및 데이터 준비

다음과 같이 라이브러리와 일별 주문 데이터인 파일 “data_for_ttest_rel.csv”를 준비한다.

1
2
3
4
5

import pandas as pd
from scipy.stats import ttest_rel

df = pd.read_csv("data_for_ttest_rel.csv")
df.head(2)

연도별 월별 주문 건수 합계가 유의미하게 차이가 나는지 확인하기 위해 다음과 같이 데이터를 가공한다.

1
2

df_g = df.groupby(["year", "month"])["order_count"].sum().reset_index()
df_g.head()

대응표본 t-검정

2023년의 월별 데이터와 2024년의 월별 데이터가 유의미하게 차이가 나는지 대응표본 t-검정을 통해 알아보자. 이를 위해 각 월별 데이터가 짝이 지어져야 한다는 점을 기억해야 한다. 지금은 데이터가 정렬이 되어있기 때문에 다음의 코드로 해결이 가능하지만, 다른 데이터를 사용하는 경우 제대로 짝이 지어지는지 확인을 하고 진행해야 하겠다.

1
2
3

ttest_rel(df_g.loc[df_g["year"] == 2023, "order_count"],
          df_g.loc[df_g["year"] == 2024, "order_count"])
## TtestResult(statistic=1.116090258112348, pvalue=0.2881708977267691, df=11)

“statistic” 이라고 되어있는 것은 검정통계량 $t$ 이며 “pvalue”는 $p\text{-}value$이다. “df”는 자유도(degree of freedom)이다. 이를 해석하면 다음과 같다.

2023년의 월별 데이터와 2024년의 월별 데이터가 유의미하게 차이가 나는지 대응표본 t-검정을 통해 알아본 결과, 검정통계량 $t$는 1.116이며 $p\text{-}value$는 0.288이다. 유의수준 5%($\alpha = 0.05$) 기준으로 판단했을 때, $p\text{-}value$가 0.288이므로 유의수준 보다 크기 때문에 귀무가설을 기각할 수 없다. 따라서 2023년의 월별 데이터와 2024년의 월별 데이터가 유의미하게 차이가 나는 것으로 보기 어렵다.

그리고 다음과 같이 2023년과 2025년 월별 데이터를 비교해보면 다음과 같다.

1
2
3

ttest_rel(df_g.loc[df_g["year"] == 2023, "order_count"],
          df_g.loc[df_g["year"] == 2025, "order_count"])
## TtestResult(statistic=-3.819409284509496, pvalue=0.00284604873310612, df=11)

2023년의 월별 데이터와 2025년의 월별 데이터가 유의미하게 차이가 나는지 대응표본 t-검정을 통해 알아본 결과, 검정통계량 $t$는 -3.819이며 $p\text{-}value$는 0.003이다. 유의수준 5%($\alpha = 0.05$) 기준으로 판단했을 때, $p\text{-}value$가 0.003이므로 유의수준 보다 작기 때문에 귀무가설을 기각할 수 있다. 따라서 2023년의 월별 데이터와 2025년의 월별 데이터는 유의미하게 차이가 난다고 할 수 있다.

그리고 ttest_rel() 산출값의 경우 일반 함수의 결과와 다른데, 다음과 같이 별도의 객체에 할당하여 확인할 수도 있다.

1
2
3
4
5
6
7
8
9

result = ttest_rel(df_g.loc[df_g["year"] == 2023, "order_count"],
                   df_g.loc[df_g["year"] == 2024, "order_count"])
result[0], result[1]
## (1.116090258112348, 0.2881708977267691)

stat, p = ttest_rel(df_g.loc[df_g["year"] == 2023, "order_count"],
                    df_g.loc[df_g["year"] == 2024, "order_count"])
stat, p
## (1.116090258112348, 0.2881708977267691)