Py) 통계 - 단일표본 t-검정

※ 본 내용에서 사용하는 iris.csv 파일은 별도로 다운로드 받아야 한다.
※ iris.csv 다운받기 [클릭]

이론

본 내용은 세 종류의 t-검정 중 첫 번째인 단일표본 t-검정에 대해 다루며 t-검정의 목록은 다음과 같다.

1. 단일표본 t-검정
2. 대응표본 t-검정
3. 독립표본 t-검정

개요

단일표본 t-검정은 모집단의 평균이 특정한 값과 같은지를 검정하는 방법이다. 예를 들어 캔맥주의 용량이 500ml로 적혀있다고 하자.

그런데 구매한 캔맥주를 까봤더니 어떤 캔에는 내용물이 좀 모자란 것 같고, 어떤 캔에는 내용물이 좀 많은 것 같을 수 있다. 이 경우에 제조사가 명시한 캔맥주의 용량 500ml이 맞는지 통계적으로 검정해보고자 할 때 단일표본 t-검정을 사용할 수 있다.

가설설정

모평균(population mean, $\mu$)이 특정한 값과 같은지를 검정하는 방법이므로 양측 검정(Two-sided test, Two-tailed test) 기준으로 다음과 같은 가설을 세울 수 있다.

● 귀무가설($H_0$) : 모집단의 평균이 표본 평균과 같다.
● 대립가설($H_1$) : 모집단의 평균이 표본 평균과 다르다.

귀무가설의 경우 “모집단의 평균이 표본 평균과 다르다고 보기 어렵다.” 라고도 쓸 수 있겠다.

각 가설을 수식으로 표현하면 다음과 같다.

검정통계량

단일표본 t-검정의 검정통계량 t는 다음과 같이 계산할 수 있다.

여기서 $\bar{X}$ 는 표본평균, $\mu$ 는 모평균, $\hat{\sigma}$ 는 표본표준편차, $n$은 표본의 크기이다.

가정

단일표본 t-검정의 가정은 다음과 같다.

• 정규성(Normality): $\bar{X}$는 평균이 $\mu$이고 분산이 $\sigma^2/n$인 정규분포를 따른다.
• 독립성(Independence): 표본의 관측값은 서로 독립이다. 즉, 표본의 관측값은 서로 영향을 주지 않는다.

유의수준, 유의확률, 기각역

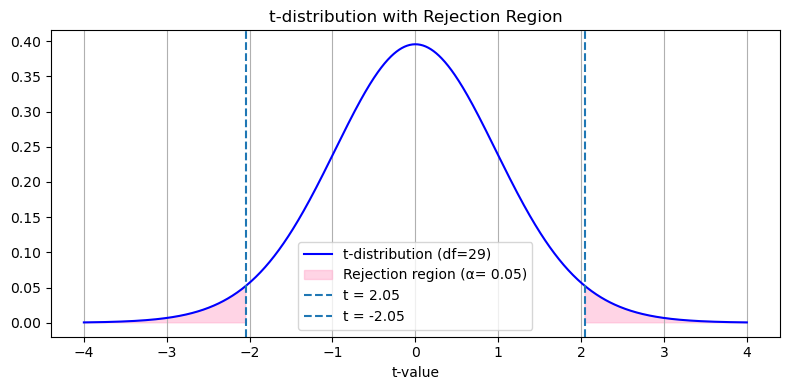
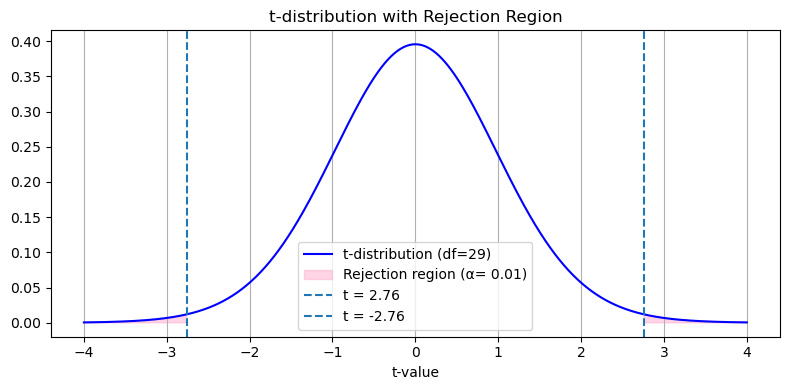
유의확률(p-value)은 귀무가설이 맞을 때 얻을 수 있는 결과보다 극단적인 결과가 나올 확률이다. 그리고 그 극단적 결과가 나올 확률에 해당하는 영역을 기각역(reject region) 보통 유의확률은 10%, 5%, 1%를 기준으로 귀무가설을 기각(reject)할지 말지를 결정한다. 이를 유의수준($\alpha$, significance level)이라고 한다. 그래서 유의확률은 유의수준 10%, 5%, 1%에 대응하는 0.1, 0.05, 0.01을 기반으로 최종 해석을 한다.

다음은 양측 검정(Two-sided test, Two-tailed test)을 기준으로 유의수준, 유의확률, 기각역을 유의수준에 따라 시각화한 결과이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# 라이브러리 및 데이터 준비
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t

plt.rcParams["figure.figsize"] = (8, 4)

val_dof = 29  
x = np.linspace(-4, 4, 1000)
y = t.pdf(x, val_dof)

val_dof = 29  
x = np.linspace(-4, 4, 1000)
y = t.pdf(x, val_dof)

# 그래프 1 - 유의수준 10%
alpha = 0.10
critical_t = t.ppf(1 - alpha / 2, val_dof)

plt.plot(x, y, "b-", label = "t-distribution (df=29)")
plt.fill_between(x, y, where = (x > critical_t) | (x < -critical_t), 
                 color = "#FFAACC", alpha = 0.5, 
                 label = f"Rejection region (α={alpha: 0.2f})")
plt.axvline( critical_t, linestyle = "--", 
            label = f"t = { critical_t:.2f}")
plt.axvline(-critical_t, linestyle = "--", 
            label = f"t = {-critical_t:.2f}")
plt.title("t-distribution with Rejection Region")
plt.xlabel("t-value")
plt.grid(True, axis = "x")
plt.legend()

plt.tight_layout()
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

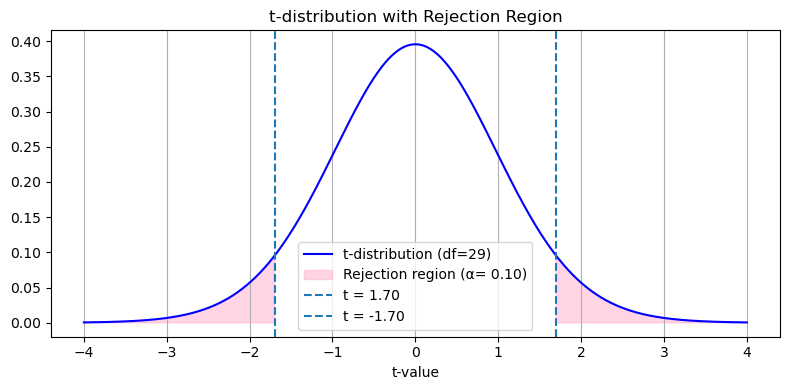
alpha = 0.05
critical_t = t.ppf(1 - alpha / 2, val_dof)

plt.plot(x, y, "b-", label = "t-distribution (df=29)")
plt.fill_between(x, y, where = (x > critical_t) | (x < -critical_t), 
                 color = "#FFAACC", alpha = 0.5, 
                 label = f"Rejection region (α={alpha: 0.2f})")
plt.axvline( critical_t, linestyle = "--", 
            label = f"t = { critical_t:.2f}")
plt.axvline(-critical_t, linestyle = "--", 
            label = f"t = {-critical_t:.2f}")
plt.title("t-distribution with Rejection Region")
plt.xlabel("t-value")
plt.grid(True, axis = "x")
plt.legend()

plt.tight_layout()
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

alpha = 0.01
critical_t = t.ppf(1 - alpha / 2, val_dof)

plt.plot(x, y, "b-", label = "t-distribution (df=29)")
plt.fill_between(x, y, where = (x > critical_t) | (x < -critical_t), 
                 color = "#FFAACC", alpha = 0.5, 
                 label = f"Rejection region (α={alpha: 0.2f})")
plt.axvline( critical_t, linestyle = "--", 
            label = f"t = { critical_t:.2f}")
plt.axvline(-critical_t, linestyle = "--", 
            label = f"t = {-critical_t:.2f}")
plt.title("t-distribution with Rejection Region")
plt.xlabel("t-value")
plt.grid(True, axis = "x")
plt.legend()

plt.tight_layout()
plt.show()

단측 검정

이전의 내용은 모두 양측 검정을 기준으로 기술한 내용들이다. 즉, 표본평균이 모평균으로부터 얼마나 떨어져있는지 검정하는 것인데, 표본평균이 모평균보다 크다거나 표본평균이 모평균부다 작은 것에 대해 검정을 하고자 한다면 단측 검정(One-sided test, One-tailed test)을 사용한다. 단측 검정에 대한 내용은 다음과 같다.

상한 단측검정(Right-tailed test): 대립가설이 특정 값보다 크다는 것을 주장할 때 사용
하한 단측검정(Left-tailed test): 대립가설이 특정 값보다 작다는 것을 주장할 때 사용

참고로 상한 단측검정과 하한 단측검정은 우측 검정(Right-tailed test) 또는 좌측 검정(Left-tailed test)으로도 부르기도 한다.

그리고 각 단측 검정의 귀무가설과 대립가설을 살펴보자. 먼저 상한 단측검정의 경우는 다음과 같다.

● 귀무가설($H_0$) : 모집단의 평균이 표본 평균보다 작거나 같다.
● 대립가설($H_1$) : 모집단의 평균이 표본 평균보다 크다.

하한 단측검정의 경우는 다음과 같다.

● 귀무가설($H_0$) : 모집단의 평균이 표본 평균보다 크거나 같다.
● 대립가설($H_1$) : 모집단의 평균이 표본 평균보다 작다.

이렇게 단측 검정의 귀무가설과 대립가설을 살펴보면, 단측 검정은 양측 검정과 달리 귀무가설과 대립가설이 서로 대칭이 아니라는 것을 알 수 있다.

논문

t-검정 관련 논문은 다음과 같다.
원문: https://seismo.berkeley.edu/~kirchner/eps_120/Odds_n_ends/Students_original_paper.pdf
정리: https://www.york.ac.uk/depts/maths/histstat/student.pdf

실습

라이브러리 및 데이터 준비

다음과 같이 라이브러리와 붓꽃 데이터인 파일 “iris.csv”를 준비한다.

1
2
3
4
5

import pandas as pd
from scipy.stats import ttest_1samp

df = pd.read_csv("data/iris.csv")
df.head(2)

그리고 Setosa 종의 데이터만 추출한다.

1
2

df_setosa = df.loc[df["Species"] == "setosa", ]
df_setosa.tail(2)

단일표본 t-검정

Setosa 종의 꽃받침 길이(Sepal Length)의 평균이 5 라는 가설을 세우고, 단일표본 t-검정을 실시해보자. 검정을 실시하기 전에 꽃받침 길이의 평균을 확인해보자.

1
2

df_setosa["SepalLength"].mean()
## 5.006

그리고 다음의 코드로 표본평균 5.006과 모평균 5와의 차이가 유의미하게 나는지 보는 코드는 다음과 같다.

1
2

ttest_1samp(df_setosa["SepalLength"], popmean = 5)
## TtestResult(statistic=0.12036212238318053, pvalue=0.9046884777690936, df=49)

“statistic” 이라고 되어있는 것은 검정통계량 $t$ 이며 “pvalue”는 $p\text{-}value$이다. “df”는 자유도(degree of freedom)이다. 이를 해석하면 다음과 같다.

Setosa 종의 꽃받침 길이(Sepal Length)의 평균($\bar{X}$)과 모평균($\mu$) 5와의 차이는 유의수준 5%($\alpha = 0.05$)기준으로 판단했을 때, $p\text{-}value$가 0.904이므로 유의수준 보다 크기 때문에 귀무가설을 기각할 수 없다. 따라서 Setosa 종의 꽃받침 길이(Sepal Length)의 평균($\bar{X}$)과 모평균($\mu$) 5와의 차이는 유의미하다고 보기 어렵다.

그리고 ttest_1samp() 산출값의 경우 일반 함수의 결과와 다른데, 다음과 같이 별도의 객체에 할당하여 확인할 수도 있다.

1
2
3
4
5
6
7

result = ttest_1samp(df_setosa["SepalLength"], popmean = 5)
result[0], result[1]
## (0.12036212238318053, 0.9046884777690936)

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 5)
stat, p
## (0.12036212238318053, 0.9046884777690936)

가끔 t-검정의 함수를 사용할 때 표본 데이터세트를 함수 내부에 넣는 것이 아니라 평균의 비교라고 해서 평균값을 넣어버리는 경우가 있는데 만약 그렇게 할 경우 다음과 같이 좋지 못한 결과가 나온다.

1
2

ttest_1samp(df_setosa["SepalLength"].mean(), popmean = 5)
## TtestResult(statistic=nan, pvalue=nan, df=0)

다음으로 모평균을 바꿔가면서 검정을 실시해보자. 모평균이 각각 4.9와 4.5일 때의 검정 결과는 다음과 같다.

1
2
3
4
5
6
7
8
9
10

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 4.9)
stat, p
## (2.1263974954361062, 0.038532176584544255)

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 4.5)
stat, p
## (10.150538987647845, 1.223035147861195e-13)

round(p, 5)
## 0.0

모평균이 4.9인 경우는 유의수준 5%를 기준으로 판단할 때 $p\text{-}value$가 5%인 0.05보다 작은 0.039이므로 귀무가설을 기각할 수 있다. 따라서 Setosa 종의 꽃받침 길이(Sepal Length)의 평균($\bar{X}$)과 모평균($\mu$) 4.9와의 차이는 유의미하다고 볼 수 있다.

모평균이 4.5인 경우는 유의수준 5% 기준으로 판단할 때 $p\text{-}value$가 5%인 0.05보다 작기 때문에 역시나 귀무가설을 기각할 수 있고 모평균과 표본평균이 통계적으로 유의미하게 차이가 난다고 볼 수 있다.

즉, 모평균이 표본평균보다 작아질수록 검정통계량 $t$가 커지고 $p\text{-}value$는 작아지는 것을 볼 수 있다. 그럼 이번엔 모평균을 표본평균보다 키워보도록 하겠다. 모평균이 각각 5.1와 5.5일 때의 검정 결과는 다음과 같다.

1
2
3
4
5
6
7

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 5.1)
stat, p
## (-1.8856732506697453, 0.06527445885090742)

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 5.5)
stat, p
## (-9.909814742881483, 2.7171271354067663e-13)

모평균이 5.1인 경우는 유의수준 5%를 기준으로 판단할 때 $p\text{-}value$가 5%인 0.05보다 큰 0.065이므로 귀무가설을 기각할 수 없다. 따라서 Setosa 종의 꽃받침 길이(Sepal Length)의 평균($\bar{X}$)과 모평균($\mu$) 5.1와의 차이는 유의미하다고 볼 수 없다.

반면 모평균 5.9의 경우는 유의수준 5% 기준으로 판단할 때 $p\text{-}value$가 5%인 0.05보다 작기 때문에 귀무가설을 기각할 수 있고 모평균과 표본평균이 통계적으로 유의미하게 차이가 난다고 볼 수 있다.

상기내용을 종합해봤을 때 표본평균이 모평균에서 멀어질수록 $p\text{-}value$가 작아지는 것을 볼 수 있다. 왜냐하면 양측검정이기 때문이다.

단측 검정의 경우

기본적으로 ttest_1samp() 함수는 이 검정 유형을 결정하는 인자 “alternative”의 기본값이 “two-sided”이다. 그래서 만약 표본평균이 모평균보다 작은 경우와 큰 경우를 따로 따로 검정하고자 한다면 단측검정을 실시해야 하는데 이 경우에는 “alternative” 인자의 값을 “less” 또는 “greater”로 지정해주면 된다. 함수의 문서에는 다음과 같이 설명이 나와있다.

• two-sided: the mean of the underlying distribution of the sample is different than the given population mean (popmean)
• less: the mean of the underlying distribution of the sample is less than the given population mean (popmean)
• greater: the mean of the underlying distribution of the sample is greater than the given population mean (popmean)

그럼 이번엔 “alternative” 인자의 값을 “less”로 지정하여 단측검정을 실시하고 모평균이 바뀔 때 $p\text{-}value$가 어떻게 바뀌는지 살펴보자.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 4.9,
                      alternative = "less")
stat, p
## (2.1263974954361062, 0.9807339117077278)

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 4.5,
                      alternative = "less")
stat, p
## (10.150538987647845, 0.9999999999999388)

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 5.1,
                      alternative = "less")
stat, p
## (-1.8856732506697453, 0.03263722942545371)

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 5.5,
                      alternative = "less")
stat, p
## (-9.909814742881483, 1.3585635677033831e-13)

모평균이 점점 커져서 표본평균이 상대적으로 더 작아질수록 $p\text{-}value$가 작아지는 것을 볼 수 있다.

그럼 이번엔 “alternative” 인자의 값을 “greater”로 지정하여 단측검정을 실시하고 모평균이 바뀔 때 $p\text{-}value$가 어떻게 바뀌는지 살펴보자.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 4.9,
                      alternative = "greater")
stat, p
## (2.1263974954361062, 0.019266088292272127)

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 4.5,
                      alternative = "greater")
stat, p
## (10.150538987647845, 6.115175739305976e-14)

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 5.1,
                      alternative = "greater")
stat, p
## (-1.8856732506697453, 0.9673627705745462)

stat, p = ttest_1samp(df_setosa["SepalLength"], popmean = 5.5,
                      alternative = "greater")
stat, p
## (-9.909814742881483, 0.9999999999998641)

모평균이 점점 작아져서 표본평균이 상대적으로 더 커질수록 $p\text{-}value$가 작아지는 것을 볼 수 있다.