Py) 통계 - 정규성 검정
Python / Stat
15분 읽기 (대략 2288 단어)

Py) 통계 - 정규성 검정

주어진 자료가 정규분포를 따르는지 확인하는 정규성 검정(Normality Test)에 대해 알아보자.

이론

개요

데이터가 정규분포(normal distribution)를 따르는지 알아보는 것은 통계분석을 위해 매우 중요한 과정이다. 정규분포를 따르지 않는다면, 통계분석 결과가 왜곡될 수 있기 때문이다. 그래서 데이터가 정규분포를 따르고 있는지 여부를 확인하는 작업이 필요하다. 그리고 분포 기반의 이상치 판별을 위해서도 정규분포를 기반으로 접근하고 해석해야 하는지, 아니면 다른 분포로 간주하고 해석해야 하는지 확실하게 하기 위해서도 정규성 검정이 필요할 수 있다.

다양한 정규성 검정

정규성 검정은 대표적으로 Shapiro-Wilk 검정, Kolmogorov-Smirnov 검정이 있으며 해당 검정은 다음과 같은 특징이 있다.

  • Shapiro-Wilk 검정
    - 표본 데이터의 순서 통계량과 해당하는 정규 분포에서 예상되는 값 사이의 상관관계를 검정
    - 이 검정은 소표본(n < 50)에 매우 효과적
    - 표본 크기가 커질수록 검정의 민감도가 떨어질 수 있음
  • Kolmogorov-Smirnov 검정
    - 표본 데이터의 누적 분포 함수(CDF)와 참조된 정규 분포의 CDF 사이의 최대 차이를 기반으로 정규성을 검정
    - 큰 표본을 대상으로 주로 활용됨
    - 기본적으로 모수가 알려져 있어야 함
    - 표본의 평균과 표준편차를 사용한다면 Liliiefors 검정을 사용하는 것을 권장

그 외에도 다양한 정규성 검정은 다음과 같다.

  • Lilliefors 검정
    - 표본으로부터 추정된 평균과 표준편차를 사용하여 정규성을 검정
    - 소표본(n < 50)의 정규성을 검정하기 위해 사용
    - 표본 크기가 커질수록 검정의 민감도가 떨어질 수 있음
    - Kolmogorov-Smirnov 검정의 확장된 버전
  • Anderson-Darling 검정
    - 이 검정은 표본의 누적 분포와 정규 분포의 누적 분포 사이의 차이를 측정
    - 특히 분포의 꼬리 부분에서의 차이에 더 민감하게 반응하는 특징이 있음
    - 정규성을 가정한 모델의 적합성을 평가할 때 유용하게 사용
  • Jarque-Bera 검정
    - 데이터의 왜도(skewness)와 첨도(kurtosis)를 이용하여 정규성을 검정
    - 주로 대표본의 정규성 검정에 사용

위의 검정들은 데이터의 정규성을 검정하기 위한 다양한 방법들로, 특정 상황이나 데이터의 특성에 따라 적합한 검정법을 선택하는 것이 중요합니다.

그 외에 데이터가 정규분포에 가까운지 알아보는 QQ-plot이 있다.

귀무가설과 대립가설

정규성 검정의 기본적인 귀무가설과 대립가설은 다음과 같다.

귀무가설($H_o$): 데이터의 분포는 정규분포와 다르다고 보기 어렵다.
대립가설($H_1$): 데이터의 분포는 정규분포와 다르다.

물론 각각의 검정 방법에 따라 귀무가설과 대립가설이 조금씩 다르나 대부분의 경우 위와 같은 귀무가설과 대립가설을 사용한다. 다음은 각 검정 방법에 따른 귀무가설과 대립가설이다.

Kolmogorov-Smirnov 검정

귀무가설($H_o$): 두 표본 집단간 분포는 같다.
대립가설($H_1$): 두 표본 집단간 분포는 다르다.

Anderson-Darling 검정

귀무가설($H_o$): 표본이 특정 분포를 따른다.
대립가설($H_1$): 표본이 특정 분포를 따르지 않는다.

Jarque-Bera 검정

귀무가설($H_o$): 표본의 왜도와 (초과)첨도는 정규 분포의 것과 같다.
대립가설($H_1$): 표본의 왜도와 (초과)첨도는 정규 분포의 것과 다르다.

좀 더 엄밀하게 말하자면 표본의 왜도와 (초과)첨도가 0인지 아닌지 검정하는 것이다.

실습

라이브러리 및 데이터 준비

다음과 같이 라이브러리와 객체를 준비한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
import seaborn as sns

np.random.seed(123)
arr_1 = np.random.normal(size = 30)
arr_1[:5]
## array([-1.0856306 ,  0.99734545,  0.2829785 , -1.50629471, -0.57860025])

arr_2 = np.random.normal(size = 30)
arr_2[:5]
## array([-0.25561937, -2.79858911, -1.7715331 , -0.69987723,  0.92746243])

arr_3 = np.random.f(10, 15, size = 30)
arr_3[:5]
## array([0.5028127 , 1.32641573, 0.49140284, 2.48931422, 0.84462236])

“arr_1” 객체와 “arr_2” 객체는 정규분포를 따르는 데이터이고 “arr_3” 객체는 F-분포를 따르는 데이터이다.
각 객체의 데이터를 시각화 해보면 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
fig, axes = plt.subplots(3, 2, figsize = (15, 10))

axes[0, 0].hist(arr_1, bins = 10, color = "blue", rwidth=0.95)
axes[0, 0].set_title("Histogram - arr_1")

sns.kdeplot(arr_1, ax = axes[0, 1], color = "blue")
axes[0, 1].set_title("Density Plot - arr_1")

axes[1, 0].hist(arr_2, bins = 10, color = "blue", rwidth=0.95)
axes[1, 0].set_title("Histogram - arr_2")

sns.kdeplot(arr_2, ax = axes[1, 1], color = "blue")
axes[1, 1].set_title("Density Plot - arr_2")

axes[2, 0].hist(arr_3, bins = 10, color = "blue", rwidth=0.95)
axes[2, 0].set_title("Histogram - arr_3")

sns.kdeplot(arr_3, ax = axes[2, 1], color = "blue")
axes[2, 1].set_title("Density Plot - arr_3")

plt.tight_layout()
plt.show()

샘플 데이터 분포

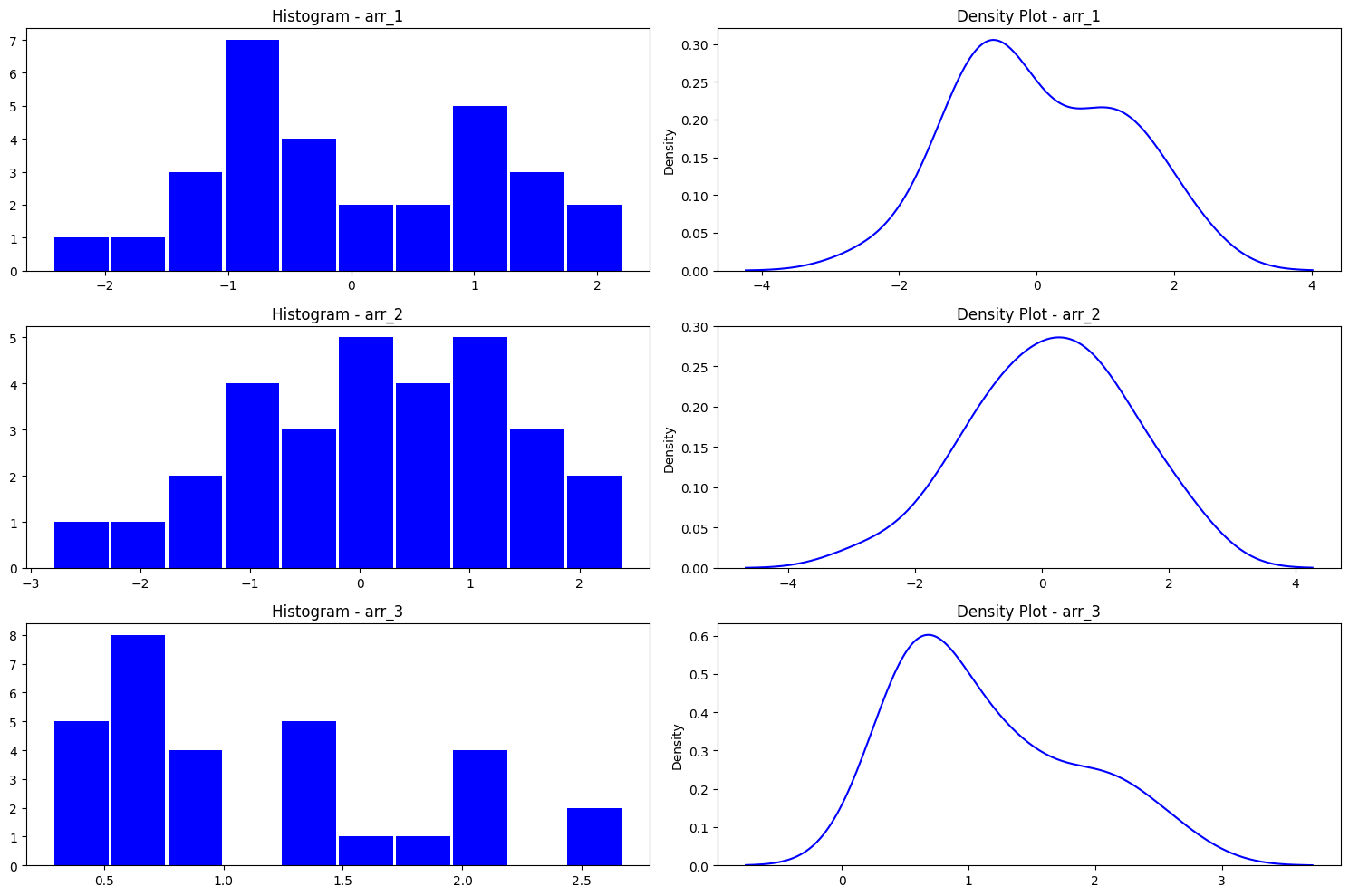
Shapiro-Wilk 검정

Shapiro-Wilk 검정을 위해서 shapiro() 함수를 사용하며 각 객체에 대한 검정 결과는 다음과 같다.

1
2
3
4
5
6
7
8
stats.shapiro(arr_1) # 검정통계량, p-value
## ShapiroResult(statistic=0.9621370434761047, pvalue=0.35087570548057556)

stats.shapiro(arr_2) # 검정통계량, p-value
## ShapiroResult(statistic=0.9874829649925232, pvalue=0.9716595411300659)

stats.shapiro(arr_3) # 검정통계량, p-value
## ShapiroResult(statistic=0.8935506343841553, pvalue=0.0058619617484509945)

검정 결과의 p-value를 보았을 때 유의수준 5% 기준으로 “arr_1”과 “arr_2”의 경우 귀무가설을 기각하지 못하고, “arr_3” 객체의 경우 귀무가설을 기각하고 대립가설을 채택하여 표본이 정규분포를 따르지 않는다고 결론을 내릴 수 있다.

Kolmogorov-Smirnov 검정

Kolmogorov-Smirnov 검정을 위해서 kstest() 함수를 사용하며 각 객체에 대한 검정 결과는 다음과 같다.

1
2
3
4
5
6
7
8
list(stats.kstest(arr_1, "norm")) # stat, p
## [0.1660065953344917, 0.3416826717395778]

list(stats.kstest(arr_2, "norm")) # stat, p
## [0.14678998077653516, 0.49213767629370864]

list(stats.kstest(arr_3, "norm")) # stat, p
## [0.631637421230662, 3.9808958610654024e-12]

검정 결과의 p-value를 보았을 때 유의수준 5% 기준으로 “arr_1”과 “arr_2”의 경우 귀무가설을 기각하지 못하고, “arr_3” 객체의 경우 귀무가설을 기각하고 대립가설을 채택하여 표본이 정규분포를 따르지 않는다고 결론을 내릴 수 있다.

상기 방법은 표준정규분포와 비교하는 것이고 만약 평균과 표준편차를 직접 지정하고 싶다면 다음과 같이 사용한다.

1
2
3
4
5
6
val_mean = 2
val_std = 3
stat, p = stats.kstest(arr_1, "norm",
                       args = (val_mean, val_std))
stat, p # 검정통계량, p-value
## (0.47958148891407104, 7.229258415526838e-07)

검정 결과의 p-value를 보았을 때 유의수준 5% 기준으로 “arr_1”은 평균이 2이고 표준편차가 3인 정규분포와는 유의미하게 다르다고 결론을 내릴 수 있다.

Liliefors 검정

Liliefors 검정을 위해서 lilliefors() 함수를 사용하며 각 객체에 대한 검정 결과는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
from statsmodels.stats.diagnostic import lilliefors

lilliefors(arr_1, dist = "norm") # 검정통계량, p-value
## (0.1550327809120738, 0.06267433158337248)

lilliefors(arr_2, dist = "norm")
## (0.061677319274631826, 0.99)

lilliefors(arr_3, dist = "norm")
## (0.17379146937757062, 0.02164780082850969)

검정 결과의 p-value를 보았을 때 유의수준 5% 기준으로 “arr_1”과 “arr_2”의 경우 귀무가설을 기각하지 못하고, “arr_3” 객체의 경우 귀무가설을 기각하고 대립가설을 채택하여 표본이 정규분포를 따르지 않는다고 결론을 내릴 수 있다.

Anderson-Darling 검정

Anderson-Darling 검정을 위해서 anderson() 함수를 사용하며 각 객체에 대한 검정 결과는 다음과 같다.

1
2
3
4
5
6
7
8
stat, arr_c, arr_lv = stats.anderson(arr_1, dist = "norm")
print(stat)
## 0.5078567066925821

df_result = pd.DataFrame([arr_c, arr_lv]).transpose()
df_result.columns = ["critical_values", "significance_level"]
df_result["reject"] = df_result["critical_values"] < stat
df_result
critical_values significance_level reject
0 0.521 15.0 False
1 0.593 10.0 False
2 0.712 5.0 False
3 0.830 2.5 False
4 0.988 1.0 False

통계량이 충분히 작아 유의수준 1% 부터 15% 기준까지 모두 귀무가설을 기각하지 못함을 알 수 있다.

1
2
3
4
5
6
7
8
stat, arr_c, arr_lv = stats.anderson(arr_2, dist = "norm")
print(stat)
## 0.12356834593997235

df_result = pd.DataFrame([arr_c, arr_lv]).transpose()
df_result.columns = ["critical_values", "significance_level"]
df_result["reject"] = df_result["critical_values"] < stat
df_result
critical_values significance_level reject
0 0.521 15.0 False
1 0.593 10.0 False
2 0.712 5.0 False
3 0.830 2.5 False
4 0.988 1.0 False

통계량이 충분히 작아 유의수준 1% 부터 15% 기준까지 모두 귀무가설을 기각하지 못함을 알 수 있다.

1
2
3
4
5
6
7
8
stat, arr_c, arr_lv = stats.anderson(arr_3, dist = "norm")
print(stat)
## 1.207822852623032

df_result = pd.DataFrame([arr_c, arr_lv]).transpose()
df_result.columns = ["critical_values", "significance_level"]
df_result["reject"] = df_result["critical_values"] < stat
df_result
critical_values significance_level reject
0 0.521 15.0 True
1 0.593 10.0 True
2 0.712 5.0 True
3 0.830 2.5 True
4 0.988 1.0 True

통계량이 커서 유의수준 1% 부터 15% 기준까지 모두 귀무가설을 기각함을 알 수 있다.

Jarque-Bera 검정

Jarque-Bera 검정을 위해서 jarque_bera() 함수를 사용하며 각 객체에 대한 검정 결과는 다음과 같다.

1
2
3
4
5
6
7
8
stats.jarque_bera(arr_1) # 검정통계량, p-value
## SignificanceResult(statistic=0.9766068804921089, pvalue=0.6136666336336749)

stats.jarque_bera(arr_2) # 검정통계량, p-value
## SignificanceResult(statistic=0.3851809149153991, pvalue=0.8248197037354764)

stats.jarque_bera(arr_3) # 검정통계량, p-value
## SignificanceResult(statistic=3.2771308782900626, pvalue=0.19425851816374295)

검정 결과 p-value가 모두 0.05보다 크므로 귀무가설을 기각하지 못함을 알 수 있다.

# , , , , , , ,
327142-eng.png
[R을 R려줘] R 데이터 시각화
326871-eng.png
[R을 R려줘] R 기초다지기

Inflearn에서 인강을 평생 소장하세요!

Py) ML - Scikit-Learn k-means 에러
Git) Copilot(VSCode)

카테고리

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×