브라이틱스(Brightics)에서 변수간 상관계수 확인이 가능한 Correlation을 알아본다.
Statistics
※ 본 내용은 Load 함수 블럭에서 bike.csv 파일을 불러온 후에 진행한다.
※ bike.csv 다운받기 [클릭]
개요
상관분석은 두 변수간 선형 관계(linear relationship, 직선적 관계)가 존재하는지, 존재하면 얼마나 강한지 알아보는 알아보는 분석 기법이다. 상관분석을 한다고 하면 보통 피어슨 상관계수(Pearson’s Correlation Coefficient)를 떠올린다. 하지만 피어슨 상관계수 말고도 어떤 속성의 자료간 비교가 이루어지는가에 따라서 알맞는 분석 기법을 선택해야 한다. 다음의 표를 참고하도록 하자.
| Quantitiative | Ordinal | Nominal | |
|---|---|---|---|
| Quantitiative | Pearson's | Biserial | Point Biserial |
| Ordinal | Biserial | Spearman/Kendall | Rank Biserial |
| Nominal | Point Biserial | Rank Biserial | Phi, L, C Lambda |
상관계수의 값에 따른 두 연속형 변수의 대략적인 분포는 다음과 같다. 모양이 직선에 가까울수록 1 또는 -1에 가까워짐을 알 수 있다.
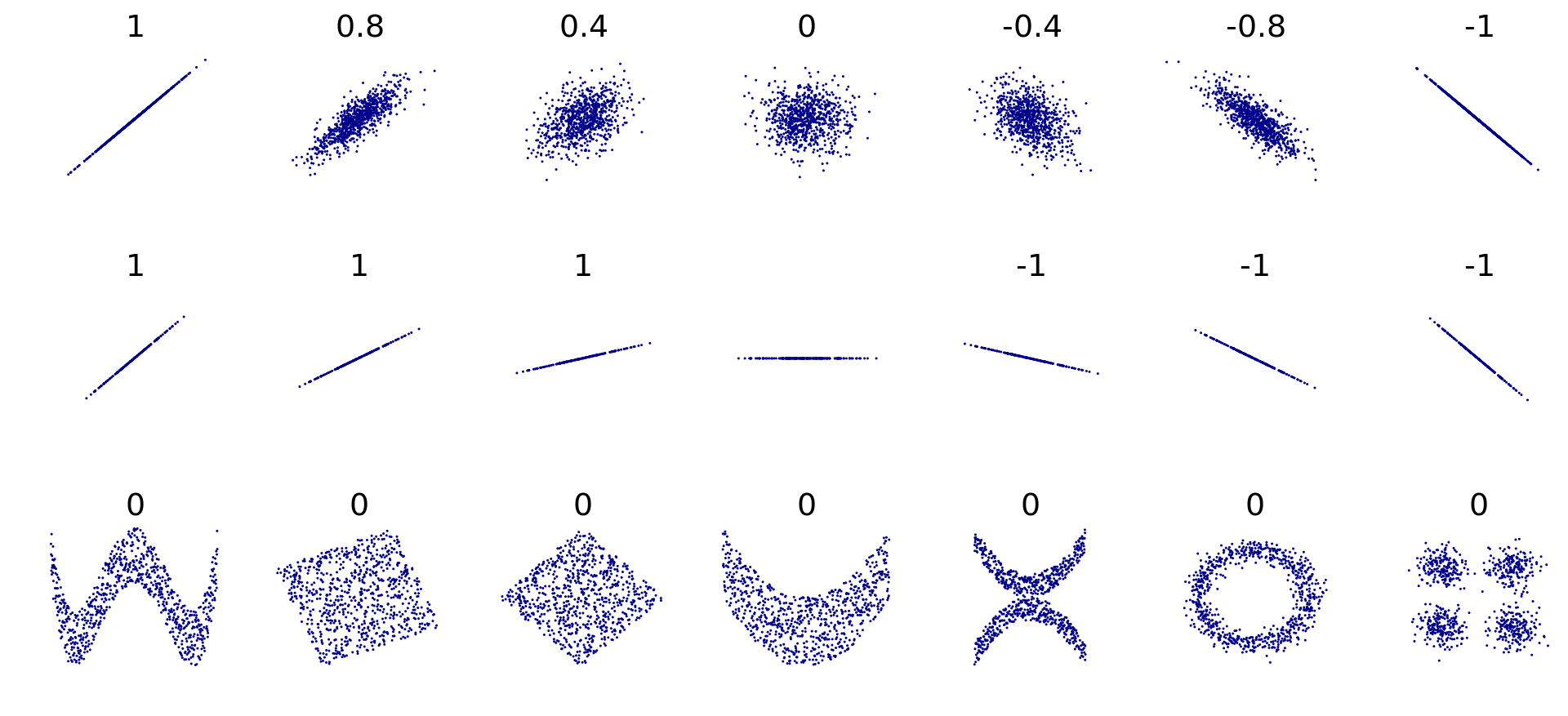
※ 출처: https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
Pearson’s Correlation
정식 명칭은 피어슨의 곱적률 상관(Pearson’s product-moment correlation)은 두 변수의 선형 관계가 존재할 경우 그 관계가 얼마나 강한지 알 수 있는 값이며 두 변수가 연속형 양적 변수일 경우에 사용가능한 방법이다. 상관계수는 공분산으로 부터 유도되며, 이를 제곱하는 경우 단순선형회귀의 결정계수와 같다. 그리고 상관계수의 값 범위는 -1 에서 1사이 이며 부호가 양수인 경우 “양의 상관 관계” 음수인 경우 “음의 상관 관계” 라고 한다.
피어슨 상관계수는 다음과 같이 계산한다.
검정통계량 t는 다음과 같이 계산한다.
p-value는 $2 \times P(T>t)$로 계산하며 여기서 T는 자유도가 n – 2인 t 분포를 따른다.
- 귀무가설($𝐻_0$): 두 변수간 선형관계가 존재하지 않는다. (r = 0)
- 대립가설($𝐻_1$): 두 변수간 선형관계가 존재한다. (r ≠ 0)
Spearman’s Correlation
스피어만 상관분석은 두 변수가 순서형 변수일 경우에 사용가능한 방법이며 두 변수가 정규성을 따르지 않는 경우에도 사용할 수 있는 비모수적 방법이다. 상관계수는 각 변수의 순위를 매긴 후 그 순위의 차를 활용하여 계산한다. 그리고 상관계수의 값 범위는 -1 에서 1사이 이며 부호가 양수인 경우 “양의 상관 관계” 음수인 경우 “음의 상관 관계” 라고 한다.
스피어만 상관계수는 다음과 같이 계산한다.
검정통계량 t는 다음과 같이 계산한다.
- 귀무가설($𝐻_0$): 두 변수간 선형관계가 존재하지 않는다. (rho = 0)
- 대립가설($𝐻_1$): 두 변수간 선형관계가 존재한다. (rho ≠ 0)
Kendall Correlation
상관분석은 두 변수가 순서형 변수일 경우에 사용가능한 방법이며 두 변수가 정규성을 따르지 않는 경우에도 사용할 수 있는 비모수적 방법이다. 그리고 상관계수의 값 범위는 -1 에서 1사이 이며 부호가 양수인 경우 “양의 상관 관계” 음수인 경우 “음의 상관 관계” 라고 한다.
켄달 상관계수는 다음과 같이 계산한다.
검정통계량 z는 다음과 같이 계산한다.
- 귀무가설($𝐻_0$): 두 변수간 선형관계가 존재하지 않는다. (tau = 0)
- 대립가설($𝐻_1$): 두 변수간 선형관계가 존재한다. (tau ≠ 0)
설정
Correlation 블럭의 설정 창은 다음과 같다.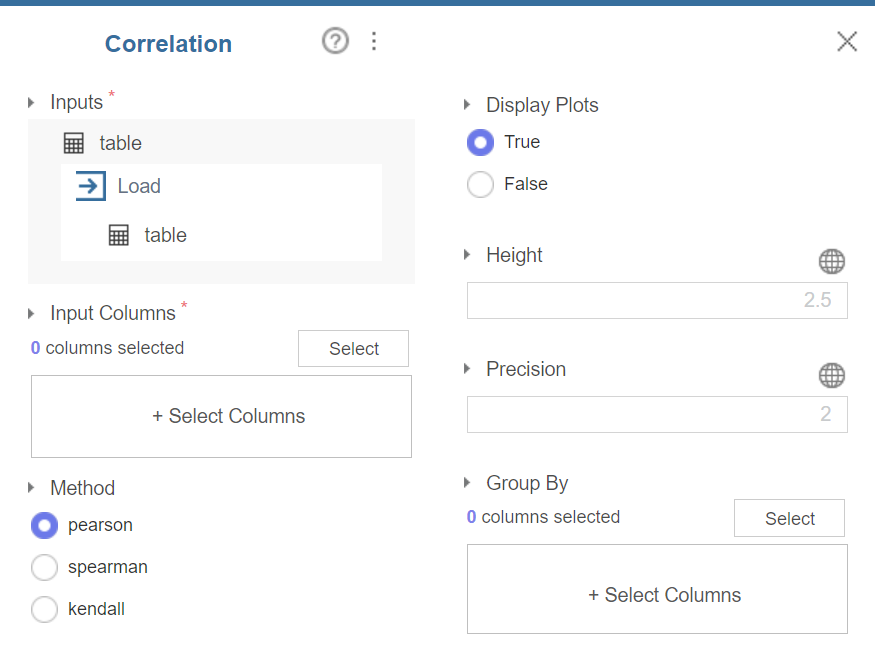
Input Columns 에는 상관분석을 실시할 변수를 지정해준다.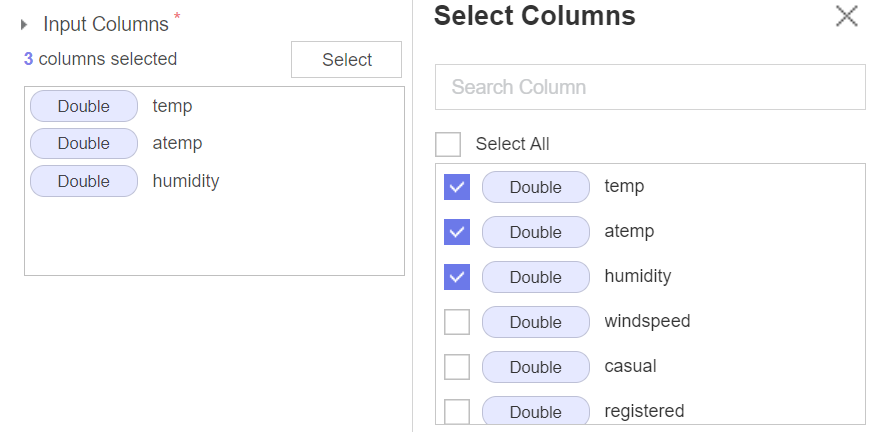
Method 에서 “pearson”, “spearman”, “kendall” 세 개 중 어떤 상관분석을 실시할지 선택할수 있다.
Display Plots 은 “True”라고 할 경우 상관계수행렬도(correlation coefficient matrix plot)을 그려준다. 그리고 해당 출력물의 크기를 Height 에 값을 입력하여 지정할 수 있고, 표기되는 상관계수를 반올림하여 소수점 몇 째 자리까지 표기할 것인지는 Precision 에 지정할 수 있다.
추가로 특정 변수의 원소를 기준으로 묶음 연산을 하고자 할 때는 대상이 되는 변수를 아래 Group By 부분에서 [Select] 버튼을 눌러 변수 목록을 불러와 선택해준다. 묶음 연산은 되도록이면 연속형 변수가 아닌 명목형 변수를 기준으로 수행을 권장한다.
결과
기온, 체감온도, 상대습도인 temp, atemp, himidity 변수로 피어슨 상관계수를 산출한 결과는 다음과 같다.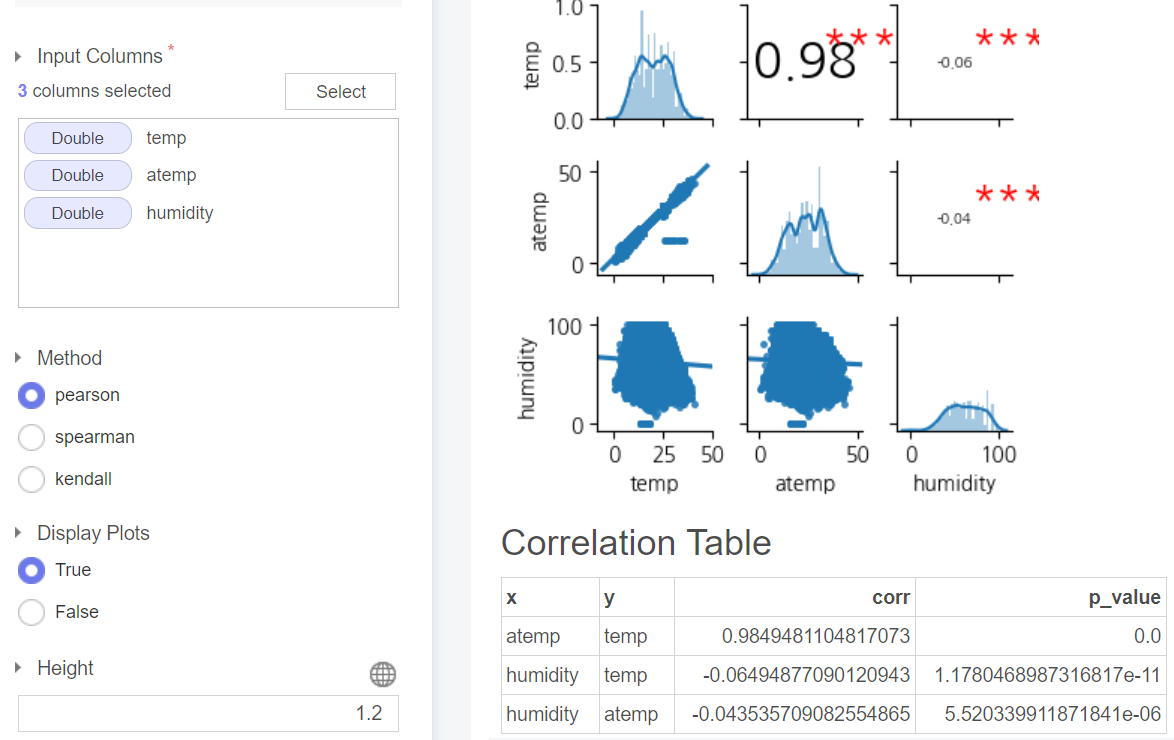
결과 오른쪽 아래 Correlation Table 이 있는데 이는 각 변수간 상관계수와 p-value가 기술되어있다. 결과를 보았을 때 유의수준 5%(0.05) 기준으로 p-value가 작아 귀무가설을 기각하고 대립가설을 채택하여 두 변수간 선형관계가 존재한다고 할 수 있으며 특히 temp 변수와 atemp 변수간 상관계수는 “0.98”이 넘기 때문에 매우 강한 양의 상관관계라고 할 수 있다.


