Br) 통계 - 등분산 검정(Bartlett's Test)

※ 본 내용은 Load 함수 블럭에서 bike.csv 파일을 불러온 후에 진행한다.
※ bike.csv 다운받기 [클릭]

개요

등분산 검정중 하나인 Bartlett 검정은 집단간 분산이 같은지 다른지 여부를 알아볼 때 사용하기도 하고 독립 2표본 t-검정 또는 일원분산분석(one-way ANOVA) 실시 전에 가정 때문에 확인하는 용도로 사용하기도 한다. 그리고 Bartlett 검정은 두 집단 뿐만 아니라 세 집단 이상에서도 사용할 수 있으며 표본이 정규성을 보일때만 사용할 수 있다.

검정 통계량 계산

• 검정통계량: $s^{2}_{i}$는 i번째 집단의 분산, $N$은 총 표본 크기, $n_{i}$는 i번째 집단의 표본 크기, $k$는 집단의 수, $s^{2}_{p}$는 합동 분산(pooled variance)이다.
  $$ T = \frac{(N-k)\ln{s^{2}_{p}} - \sum_{i=1}^{k} (N_{i} - 1) \ln{s^{2}_{i}}}{1 + (1/(3(k-1)))((\sum_{i=1}^{k}{1/(N_{i} - 1))} - 1/(N-k))} $$

참고로 $s^{2}_{p}$으로 표기된 합동 분산(pooled variance)은 다음과 같이 정의된다.

가설

- 귀무가설($H_0$): 집단간 분산이 같다.
- 대립가설($H_1$): 적어도 두 집단간 분산이 다르다.

설정

Bartlett's Test 블럭의 설정 창은 다음과 같다.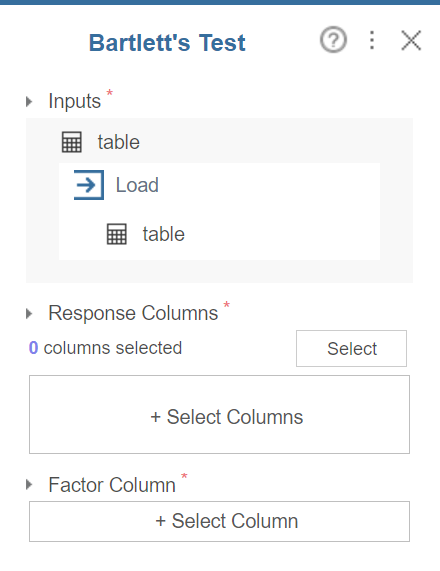

Response Columns 에는 분산을 알아보고자 하는 수치형 변수를 지정한다.
Factor Column 에는 Response Columns 에 지정한 수치형 변수를 각 집단으로 분할하는 범주형 변수가 권장된다.
각 창의 네모칸을 누르게 되면 다음과 같이 변수를 지정할 수 있다.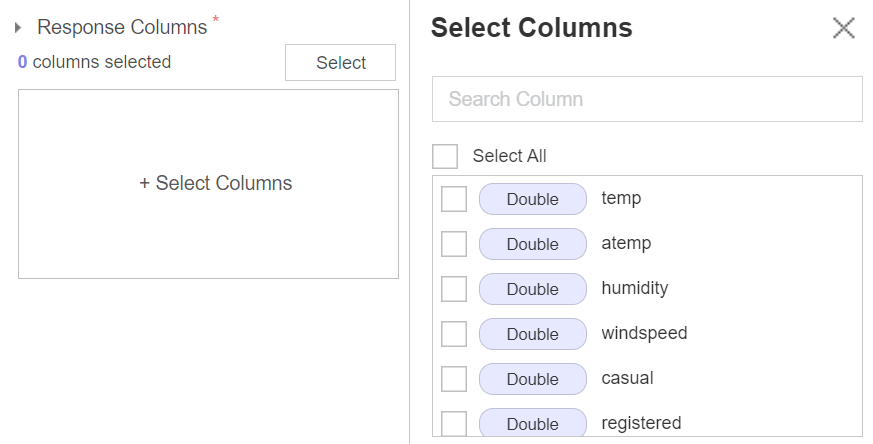

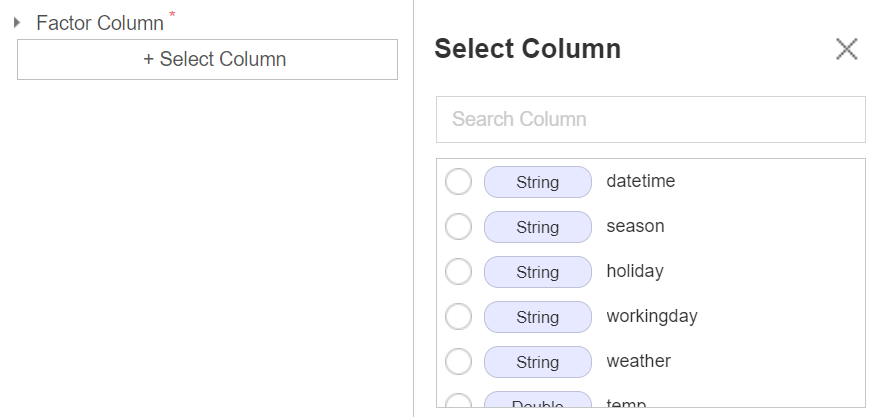
결과

일일권으로 대여한 자전거 대여수를 의미하는 casual 변수를 종속변수로 하고 분기를 구분하는 season 변수를 독립변수로 하여 분기별 일일권 자전거 대여수의 분산이 같은지 다른지 검정한 결과는 다음과 같다.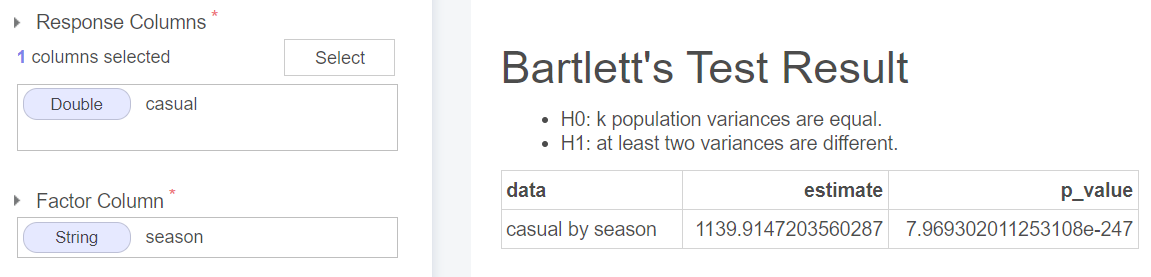

결과 중 estimate 는 검정통계량이고 p_value 는 p-value인데 이때 p-value가 7.969e-217로 유의수준 $\alpha$가 5%(0.05)일 때, p-value가 유의수준보다 작기 때문에 귀무가설을 기각하고 대립가설을 채택하여 적어도 두 집단간 분산이 다르다고 할 수 있다.