브라이틱스(Brightics)에서 두 집단의 분산 차이를 검정하는 F Test for Stacked Data를 알아본다.
Statistics
※ 본 내용은 Load 함수 블럭에서 bike.csv 파일을 불러온 후에 진행한다.
※ bike.csv 다운받기 [클릭]
개요
F-검정은 두 표본 집단의 분산을 비교하여 두 모집단의 분산의 차이가 유의미하게 나는지 검정하는 방법이다.
검정 통계량 계산
F-검정의 검정통계량 F는 두 표본 집단의 분산의 비로 산출하며 그 식은 다음과 같다.
가설
- 귀무가설($H_0$): 집단간 분산이 같다.
- 대립가설($H_1$): 집단간 분산이 다르다.
상기 귀무가설은 두 집단간 분산의 비율 F가 1 로 바꿔 말할 수 있고, 대립가설은 두 집단간 분산의 비율 F가 1이 아님 으로 바꿔 말할 수 있으니 참고하도록 하자.
설정
F Test for Stacked Data 블럭의 설정 창은 다음과 같다.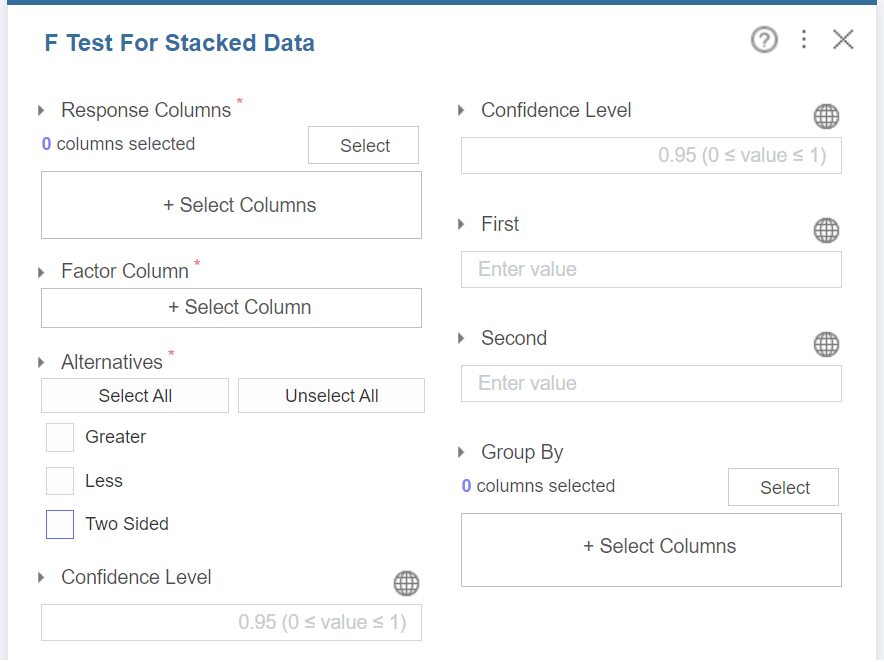
Response Columns 에는 분산을 알아보고자 하는 수치형 변수를 지정한다.
Factor Column 에는 Response Columns 에 지정한 수치형 변수를 각 집단으로 분할하는 범주형 변수가 권장된다. 단, Factor Column 에 입력되는 변수의 요인 수준(factor level)은 두 개여야 한다.
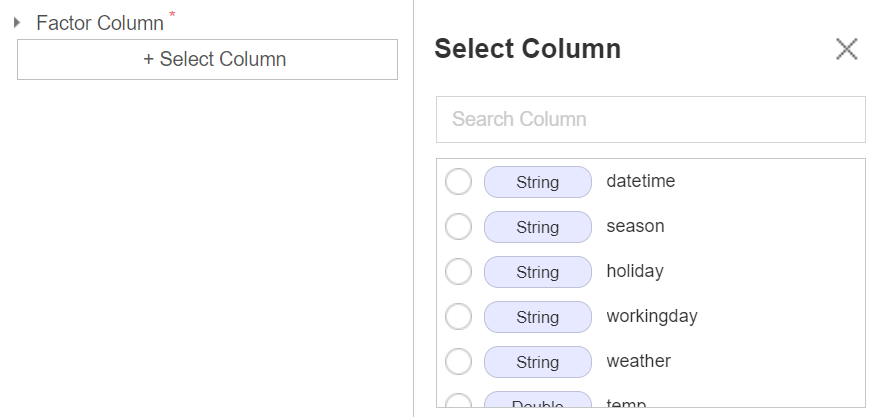
각 창의 네모칸을 누르게 되면 다음과 같이 변수를 지정할 수 있다.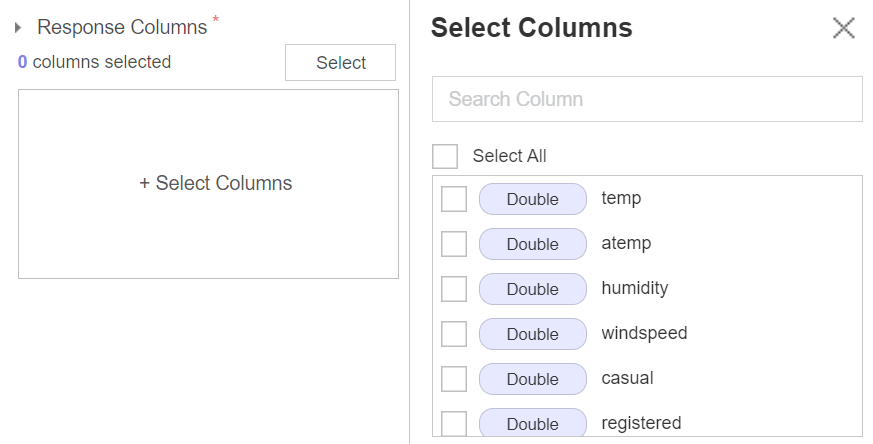
결과
정기권 대여를 의미하는 registered 변수를 종속변수로 하고 공휴일 여부를 뜻하는 holiday 변수를 독립변수로 하여 분석한 결과는 다음과 같다.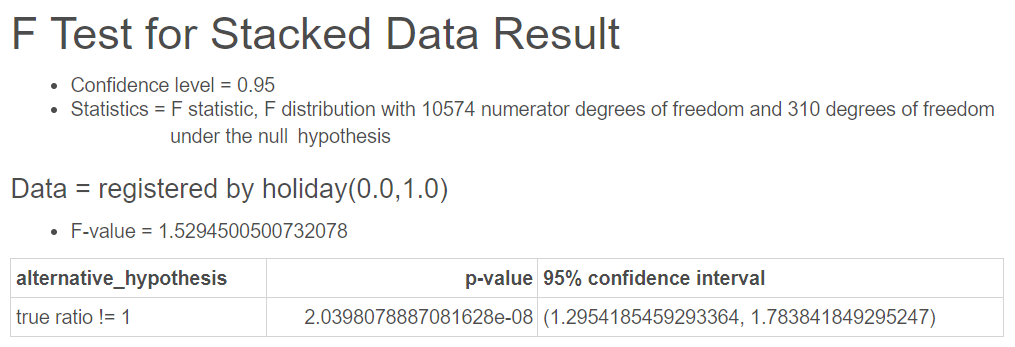
결과 중 F-value 는 검정통계량이고 p_value 는 p-value인데 이때 p-value가 2.0398e-08로 유의수준 $\alpha$가 5%(0.05)일 때, p-value가 유의수준보다 작기 때문에 귀무가설을 기각하고 대립가설을 채택하여 적어도 두 집단간 분산이 다르다고 할 수 있다.


