브라이틱스(Brightics)에서 정규성 검정을 실시하고자 할 때 사용하는 Normality Test를 알아본다.
Statistics
※ 본 내용은 Load 함수 블럭에서 normality_test_sample_2000EA.csv 파일을 불러온 후에 진행한다.
※ normality_test_sample_2000EA.csv 다운받기 [클릭]
개요
정규성 검정(Normality Test)은 주어진 표본분포가 정규분포를 따르는지 그렇지 않은지 확인하는 검정이다. 정규성 검정은 여러방법이 있지만 대표적으로 Q-Q plot을 확인하는 방법을 언급하곤 한다. Q-Q plot의 정식 명칭은 Quantile-Quantile plot, 정규분포 분위수 대조도 이며 표본을 표준정규분포의 분위수와 대조하며 그리는 그림이다. 다음의 그림에서 볼 수 있는 Q-Q plot 예시의 왼쪽 그림의 경우 각 점이 대각 점선에 대부분 몰려있는 것을 보아 모집단이 정규성을 따른다고 할 수 있다.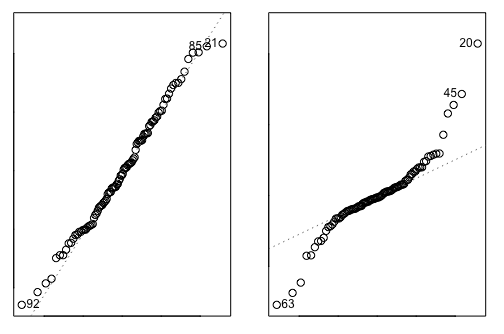
오른쪽의 경우 점선으로된 대각선에서 각 점이 많이 떨어져있기 때문에 모집단이 정규성을 따른다고 보기 어렵다. 그런데 이렇게 눈대중으로 판단하는 것은 대략적인 판단이기 때문에 조금 더 정확하게 보고자 한다면 그래프 기반의 방법이 아니라 가설검정 기반의 각종 검정법으로 접근하는 것이 좋다.
Brightics의 Normality Test 함수 블럭에서는 Kolmogorov-Smirnov Test , Jarque-Bera Test , Anderson Darling Test 이렇게 세 가지 방법을 제공하고 있다.
가설
각 검정은 엄밀하게 원리나 접근법이 다르지만 귀무가설과 대립가설은 대략 다음과 같다고 보면 된다.
- 귀무가설($H_0$): 표본 분포는 정규분포를 따른다.
- 대립가설($H_1$): 표본 분포는 정규분포를 따르지 않는다.
설정
Normality Test 블럭의 설정 창은 다음과 같다.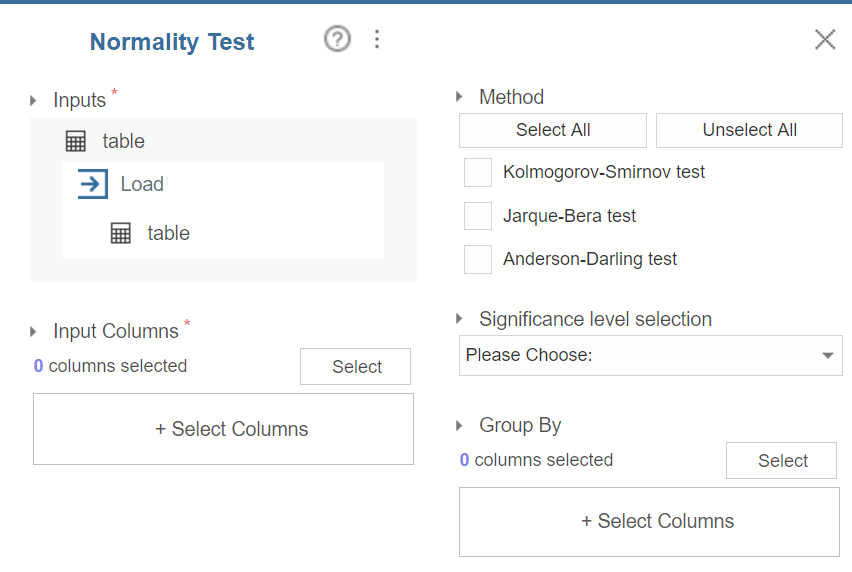
Input Columns 의 아래 네모 상자를 클릭하면 정규성 검정을 실시할 수치형 변수의 목록이 오른쪽에 뜬다. 대상 변수를 선택하여 분석을 진행한다.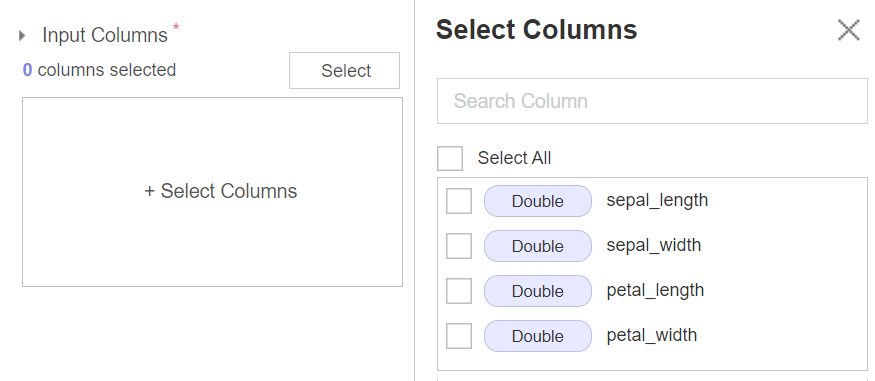
Method 에는 “Kolmogorov-Smirnov Test”, “Jarque-Bera Test”, “Anderson Darling Test” 중 어떤 분석을 실시할 것인지 선택할 수 있다.
Significance level selection 에는 다음과 같이 유의수준을 지정할 수 있다. 하지만 어차피 p-value를 보면 되기 때문에 별다른 효용은 없다.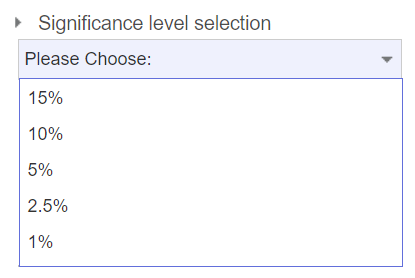
추가로 특정 변수의 원소를 기준으로 묶음 연산을 하고자 할 때는 대상이 되는 변수를 아래 Group By 부분에서 [Select] 버튼을 눌러 변수 목록을 불러와 선택해준다. 묶음 연산은 되도록이면 연속형 변수가 아닌 명목형 변수를 기준으로 수행을 권장한다.
결과
정규성 검정 결과는 다음과 같으며, Kolmogorov-Smirnov 검정 결과의 p-value가 0.3154인 것을 보아 귀무가설을 기각하지 못하여 주어진 표본 분포가 정규분포를 따른다고 할 수 있다.


