Py) ML - 모델 평가(분류모델)

개요

로지스틱 회귀, 분류나무 등 분류모델을 평가하기 위해서는 다양한 접근이 있을 수 있다. 그 중에서도 종속변수를 기반으로 확인 가능한 정분류 결과와 오분류 결과를 취합한 혼동행렬(Confusion Matrix)로 산출하는 지표 일부에 대해 알아보고자 한다.

다음은 위키피디아에 있는 혼동행렬 문서에는 다음과 같이 다양한 지표를 소개하고 있다.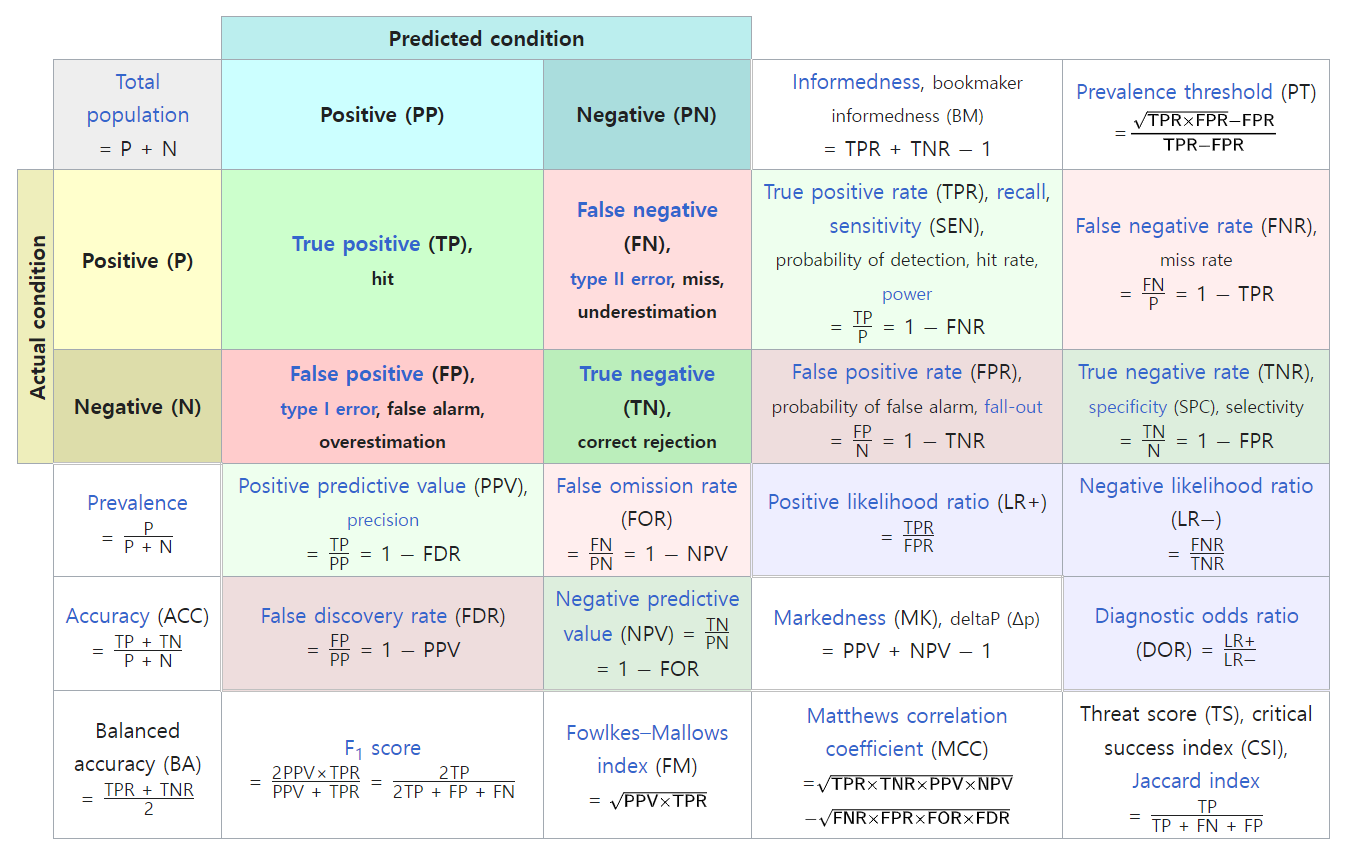

각 지표마다 사용처와 장담점이 있지만 여기에서는 그 중 비교적 자주 사용되는 지표를 알아보고자 한다.

Accuracy

정확도(Accuracy)는 올바르게 분류한 결과(True Positive, True Negative)의 비율이다.
$$Accuracy = \frac{T_P + T_N}{T_P + T_N + F_P + F_N}$$

대중적인 분류지표로 해석이 쉬우나 $T_p$만 따로 볼 수 없어 아쉬운 부분이 있다.

Precision

정밀도(Precision)는 Positive라고(True Positive, False Positive) 예측한 것 중에서 실제로 Positive인 것(True Positive)의 비율이다. 그리고 정밀도는 PPV(Positive Predictive Value)로도 부른다.
$$Precision = \frac{T_P}{T_P + F_P}$$

정밀도는 위양성(僞陽性, 거짓 양성)을 최소화하기 위해 사용되기도 하며 위양성은 1종 오류 라고도 한다.

Recall

재현율(Recall)은 실제 Positive(True Positive, False Negative) 중에서 Positive로(True Positive) 올바르게 분류한 비율이다. 그리고 재현율은 민감도(Sensitivity) 또는 TPR(True Positive Rate)으로도 부른다.
$$Recall = \frac{T_P}{T_P + F_N}$$

재현율은 위음성(僞陰性, 거짓 음성)을 최소화하기 위해 사용되기도 하며 위음성은 2종 오류 라고도 한다.

F1 score

F1 score는 정밀도와 재현율의 조화 평균으로 산출되며 F-beta score의 beta값이 1인 경우이다.
$$F1 \ score = \frac{2}{\frac{1}{Precision} + \frac{1}{Recall}} = 2 \times \frac{Recall \times Precision}{Recall + Precision}$$

F1 score는 계산에 정밀도와 재현율이 같이 균형적으로 들어가기 때문에 1종 오류와 2종 오류를 같이 고려하면서 진양성(眞陽性, True Positive)을 중점적으로 보고자 할 때 사용하기 좋은 지표이다. 그리고 정밀도와 재현율의 비율을 조정하고자 한다면 F-beta score를 보는 것이 좋다.

실습

다음과 같이 데이터프레임 객체 “df_y”를 준비한다.

1
2
3

df_y = pd.DataFrame(dict(y_true = [1, 1, 0, 0, 0, 0, 1, 1, 1, 0],
                         y_pred = [1, 0, 0, 0, 1, 0, 0, 1, 1, 0]))
df_y

“y_true” 변수의 원소는 원 데이터의 종속변수이고, “y_pred”는 모델로부터 산출된 예측값이라고 하고 다음 실습을 진행한다.

직접 계산하기

앞에서 생성한 객체 “df_y”과 crosstab() 함수를 사용하여 혼동행렬을 만들어보자.

1
2

df_tab = pd.crosstab(df_y["y_true"], df_y["y_pred"])
df_tab

혼동행렬을 정리해보면 다음과 같다.

이제 각 지표를 산출해보자.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

val_acc = df_tab.values.diagonal().sum() / df_tab.values.sum()
val_acc
## 0.7

val_pre = df_tab.iloc[1, 1] / df_tab.iloc[:, 1].sum()
val_pre
## 0.75

val_rec = df_tab.iloc[1, 1] / df_tab.iloc[1, ].sum()
val_rec
## 0.6

val_f1 = 2 / (1 / val_pre + 1 / val_rec)
val_f1
## 0.6666666666666666

sklearn 라이브러리 활용

먼저 지표산출을 위한 sklearn 라이브러리의 관련 함수를 불러온다.

1
2
3
4

from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score

이제 각 지표를 계산해보자.

1
2
3
4
5
6
7
8
9
10
11

accuracy_score(y_true = df_y["y_true"], y_pred = df_y["y_pred"])
## 0.7

precision_score(y_true = df_y["y_true"], y_pred = df_y["y_pred"])
## 0.75

recall_score(y_true = df_y["y_true"], y_pred = df_y["y_pred"])
## 0.6

f1_score(y_true = df_y["y_true"], y_pred = df_y["y_pred"])
## 0.666666666666666