R) Base Plot - k-Means 학습
R / visualization
13분 읽기 (대략 1948 단어)

R) Base Plot - k-Means 학습

머신러닝기법 중 k-Means 클러스터링 기법 학습 과정을 R의 기본 그래프로 구현한 사례를 소개하고자 한다.

개요

본 코드는 약 10년전 부터 인터넷에 떠돌던 k-Means 시각화 코드를 리펙토링한 코드이다. 사실은 강의자료 제작에 있어 저작권 문제를 피하기 위해 k-Means 움짤을 찾던 중 그냥 코드를 싹 바꿔서 새로 그려버렸다. 대충 2시간 남짓 투자해서 원하는 만큼 뒤바꾸진 못했기에 마지막에 한계점 및 향후 개선방향에 아쉬운 점을 기술하였다.

컨셉

구현 코드는 크게 세 부분으로 나뉘어져 있다.

  1. 데이터 생성부
  2. 군집 계산부
  3. 시각화부

데이터는 기본적으로 4개의 군집을 기반으로 생성되며, 특정 점을 기준으로 반경r 만큼의 원 내부에 데이터가 배치되는 꼴이다. 그리고 군집 계산의 경우 각 군집의 중심점인 centroid의 계산과 해당 군집에 속하는 데이터를 찾고 중심점 이동을 측정하기 위한 거리계산이 주된 요소이다. 계산부에서 산출한 중심점과 해당 중심점과 가까운 데이터 정보를 기반으로 점을 찍고 색을 입힌다.

Package

gif 파일을 생성하기 위해 animation 패키지를 사용한다.

1
library("animation")

UDF - Sub

Data Generation

데이터를 생성하면서 x축 좌표값을 입력 받아서 그에 맞는 y값을 할당하여 최종적으로 각 군집의 데이터가 원형으로 분포되도록 한다.

1
2
3
4
5
6
cal_y = function(x, radius, cent_x, cent_y){
  value = runif(n = 1, 
                min = -(sqrt((radius)^2 - (x - cent_x)^2) + cent_y) + 2 * cent_y, 
                max =   sqrt((radius)^2 - (x - cent_x)^2) + cent_y)
  return(value)
}

Iteration

특정 값과 중심점 사이의 거리를 유클리드 거리(Euclidean Distance) 기반으로 계산하고 그 결과를 향후 데이터의 군집 할당에 활용한다.

1
2
3
4
5
get_distances = function(x, k, centroids){
  val_dist = sqrt((x[1] - centroids[1:k, 1])^2 + # x
                  (x[2] - centroids[1:k, 2])^2)  # y 
  return(val_dist)
}

다음의 함수 cal_centroids() 는 전체 데이터와 군집정보를 입력받아 특정 군집의 centroid를 계산(평균)한다.

1
2
3
4
5
cal_centroids = function(i, data, cl_current){
  vec_centroid = c(mean(data[cl_current == i, 1]), # x
                   mean(data[cl_current == i, 2])) # y
  return(vec_centroid)
}

다음의 함수 cal_delta() 는 기존의 centroid와 연산 이후 centroid를 기반으로 유클리드 거리(Euclidean Distance)를 계산하여 centroid가 얼마나 이동했는지 확인한다.

1
2
3
4
5
6
cal_delta = function(i, data, cl_new){
  dist_x = (cl_new[i, 1] - data[i, 1])^2
  dist_y = (cl_new[i, 2] - data[i, 2])^2
  distance = sqrt(dist_x + dist_y)
  return(distance)
}

그래프

각 군집의 중심점을 빨간 점으로 표기하기 위한 함수 plot_centroid() 는 다음과 같다.

1
2
3
4
# plotting the centroids on the graph
plot_centroids = function(i, data){
  points(data[i, 1], data[i, 2], pch = 16, cex = 1.5, col = "#FF0000")
}

UDF - Main

“span” 객체에 할당된 값을 기반으로 각 군집의 중심점을 지정하고, “radius” 객체에 할당된 값을 기반으로 각 군집의 데이터 분포 정도를 지정한다. 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
kmeans_k4_gif = function(span = 3, radius = 4, n = 500, tol = 0.01, max_iter = 50){
  k = 4

  #### data generation ####
  
  # group 1
  cent_x = span
  cent_y = span
  x = runif(n = n, 
            min = cent_x - radius, 
            max = cent_x + radius)
  y = apply(as.matrix(x), MARGIN = 1, 
            FUN = "cal_y", radius = radius, cent_x = cent_x, cent_y = cent_y)
  g1 = cbind(x, y, 
             group = 1)
  
  # group 2
  cent_x = -span
  cent_y =  span
  x = runif(n = n, 
            min = cent_x - radius, 
            max = cent_x + radius)
  y = apply(as.matrix(x), MARGIN = 1, 
            FUN = "cal_y", radius = radius, cent_x = cent_x, cent_y = cent_y)
  g2 = cbind(x, y, 
             group = 2)
  
  # group 3
  cent_x = -span
  cent_y = -span
  x = runif(n = n, 
            min = cent_x - radius, 
            max = cent_x + radius)
  y = apply(as.matrix(x), MARGIN = 1, 
            FUN = "cal_y", radius = radius, cent_x = cent_x, cent_y = cent_y)
  g3 = cbind(x, y, 
             group = 3)
  
  # group 4
  cent_x =  span
  cent_y = -span
  x = runif(n = n, 
            min = cent_x - radius, 
            max = cent_x + radius)
  y = apply(as.matrix(x), MARGIN = 1, 
            FUN = "cal_y", radius = radius, cent_x = cent_x, cent_y = cent_y)
  g4 = cbind(x, y, 
             group = 4)
  
  df_data = as.data.frame(rbind(g1, g2, g3, g4))
  
  #### clustering ####
  
  # select k centroids
  centroids_indicies = sample(c(1:length(df_data[, 1])), size = k, replace = FALSE)
  centroids = df_data[centroids_indicies, 1:2]
  
  # initialize params
  delta_mean = 10
  num_iter = 0
  
  # plot margins
  par(mar = c(2, 2, 2, 2))
  
  while(delta_mean > tol && num_iter < max_iter){
    
    # calculate the distance between each point and centroids
    distance = t(apply(df_data, MARGIN = 1, 
                       FUN = "get_distances", k = k, centroids = centroids))
    
    # assign each point to a cluster
    current_cluster = apply(distance, MARGIN = 1, FUN = "which.min")
    
    # find the new centroids
    new_centroids = t(apply(matrix(1:k), MARGIN = 1, 
                            FUN = "cal_centroids", data = df_data, cl_current = current_cluster))

    # plotting 
    plot(x = df_data[, 1], 
         y = df_data[, 2], 
         col = current_cluster, 
         pch = 3, cex = 0.5, 
         xaxt = "n", yaxt = "n", xlab = "", ylab = "", # remove axis things
         main = paste0("k-Means Clustering (iter: ", num_iter, ")"))
    
    apply(as.matrix(1:k), MARGIN = 1, FUN = "plot_centroids", data = new_centroids)
    sapply(matrix(1:k), FUN = "plot_centroids", data = new_centroids)
    
    # calculate how much each centroid moved
    delta = sapply(1:k, FUN = "cal_delta", data = centroids, cl_new = new_centroids)
    delta_mean = mean(delta)
    
    centroids = new_centroids # update centroids
    
    num_iter = num_iter + 1
  }
}

실행 및 저장

animation 패키지의 saveGIF() 함수를 사용한다. 함수의 “movie.name” 인자 기본 값이 “animation.gif”으로 되어있기 때문에 작업폴더에 “animation.gif”가 생성된다.

1
2
saveGIF(kmeans_k4_gif(), interval = 0.01, 
        width = 650, height = 450)

산출물 예시

출력된 결과 이미지는 다음과 같다.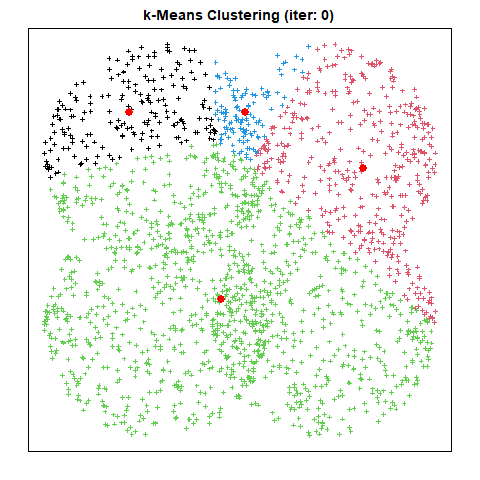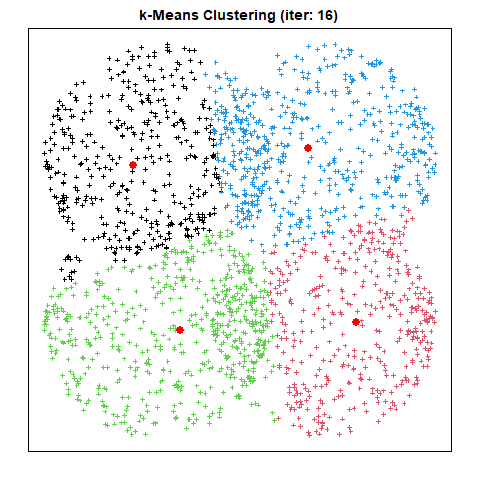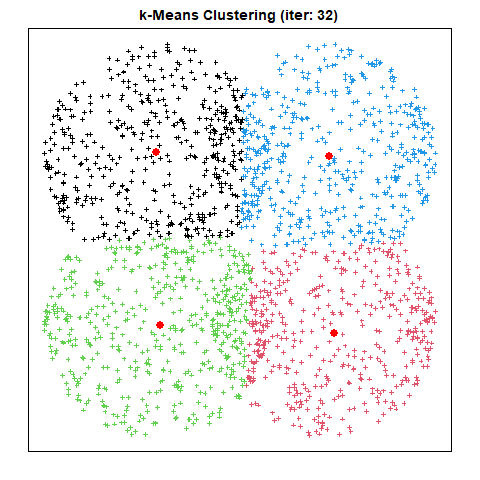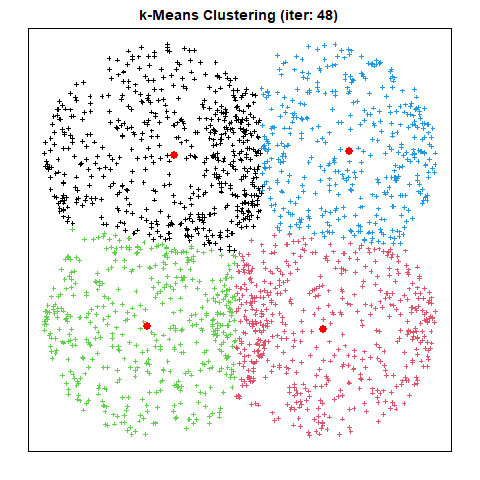
k-Means 애니메이션 예시

한계점 및 향후 개선 방향

연산부

지금 여러 연산이 별도의 사용자 정의 함수 기반으로 진행되고 있다. 예를 들어 cal_centroids() 함수의 경우 각각의 클러스터별로 apply() 류 함수 기반의 코드로 연산을 하고 있는데 이 대신 하나의 객체로 합친 후 aggregate() 라던지 dplyr 패키지의 groupby() 함수를 활용한 연산을 할 수 있겠다. 아무튼 개별 연산과 관련된 하위 사용자 정의 함수를 통합하거나 연산 대상의 객체를 병합하여 한 번에 계산하게 하면 보다 빠르고 간결한 코드가 될 것이다.

객체 속성

연산의 효율이 있을 수 있으나 과연 matrix객체가 이 연산에 굳이 필요할까 라는 생각이다. 이를 전부 data.frame/data.table/tibble 같은 객체로 바꾸면 코드 유지보수 측면에서는 확실히 이점이 있지 않을까 한다. 그리고 data.table의 경우 병렬연산이 되니 속도 향상 또한 기대할 수 있겠다. 물론 사용하는 데이터가 확실히 커진다는 전제가 선행되어야 한다.

그래프

기본 그래프가 plot() 함수를 실행할 때 마다 기존의 그래프 위에 새로운 데이터나 표기를 하기 때문에 상기와 같이 코드가 작성되었으나 이를 ggplot2 기반으로 리팩토링 하려면 몇 시간 고민을 해야 할 것 같다.

군집 개수 설정

현재 4개의 군집을 기준으로 함수가 만들어져있다. 하지만 군집 개수를 사용자가 임의로 선정하고 그에 따른 데이터도 생성하면 더 좋을 것이다. 각 군집의 개수에 비례해서 데이터 생성 기준점을 다각형의 꼭지점으로 한다던지, 데이터 생성 기준점 위치를 특수하게 지정할 수 있다던지 아직 함수가 일반화 되기엔 제약사항이 많은 것이 현실이다.

사용자 정의 함수

군집이 4개 있어서 군집별 데이터 생성 코드가 거의 중복에 가깝다. 이 부분을 별도의 사용자 정의 함수로 만들거나 하면 향후 군집개수가 변경될 경우 기민하게 대처할 수 있을 것으로 예상된다. 그리고 필요시 결과 재현을 위한 seed 설정이 추가되어도 좋을듯 하다.

# , , , , , , , ,
327142-eng.png
[R을 R려줘] R 데이터 시각화
326871-eng.png
[R을 R려줘] R 기초다지기

Inflearn에서 인강을 평생 소장하세요!

R) RStudio 1.4 업데이트
R) ggplot2 - y축 절단(1편)

카테고리

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×