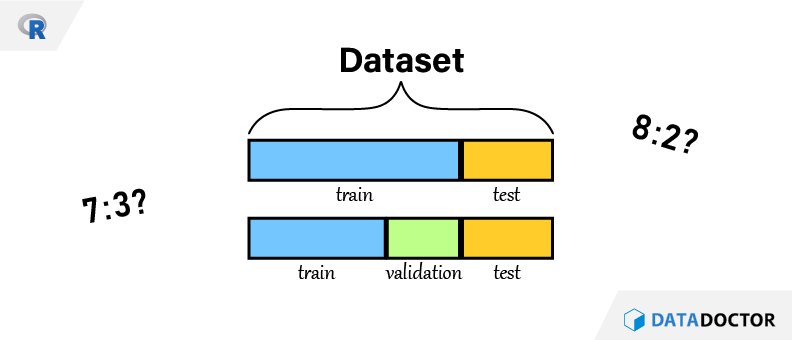
R) ML - train, test 데이터세트 분리
R / ML
10분 읽기 (대략 1452 단어)

R) ML - train, test 데이터세트 분리

머신러닝을 모델링을 할 때 데이터 전처리가 끝난 이후 꼭 하는 것이 있다. 바로 학습(train) 데이터세트와 평가(test) 데이터세트 분리이다. 7:3인지? 8:2인지? 그리고 validation set은 또 무엇인지 알아보도록 하자.

데이터세트 준비

ggplot2 패키지의 diamonds 데이터로 실습하도록 하겠다.

1
2
3
4
5
6
library("ggplot2")
df = as.data.frame(diamonds)
head(df, 2)
##   carat     cut color clarity depth table price    x    y    z
## 1  0.23   Ideal     E     SI2  61.5    55   326 3.95 3.98 2.43
## 2  0.21 Premium     E     SI1  59.8    61   326 3.89 3.84 2.31

기본 함수 사용

sample() 함수를 사용해보겠다. 정확하게 몇 개를 나눈다면 sample() 함수의 size 인자를 사용하면 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
set.seed(123)
idx_train = sample(1:nrow(df), size = 40000)
df_train = df[idx_train, ]
head(df_train)
##       carat   cut color clarity depth table price    x    y    z
## 51663  0.73 Ideal     I     VS1  60.7    56  2397 5.85 5.81 3.54
## 2986   0.70 Ideal     G     VS1  60.8    56  3300 5.73 5.80 3.51
## 29925  0.31 Ideal     D     VS1  61.6    55   713 4.30 4.33 2.66
## 29710  0.31 Ideal     H    VVS1  62.2    56   707 4.34 4.37 2.71
## 37529  0.31 Ideal     E      IF  60.9    55   987 4.39 4.41 2.68
## 2757   0.83  Good     E     SI1  63.7    59  3250 5.95 5.89 3.77

nrow(df_train)
## [1] 40000

그럼 학습 데이터세트는 만들었으니 평가 데이터세트를 추출해보자. 숫자가 작으면 손으로라도 하겠지만 당장 학습 데이터세트를 추출하기 위한 색인(index)숫자가 4만개라 여의치 않다.
그럼 집합으로 접근하는 것은 어떨까? 어차피 전체 집합에서 학습 데이터세트의 색인을 추출했기 때문에 이의 여집합을 보면 될 것이다. R 기본함수 중 집합관련 함수 setdiff() 함수를 사용하면 다음과 같다.

1
2
setdiff(x = 1:5, y = c(1, 2, 4))
## [1] 3 5

전체 집합에 해당하는 원소를 인자 x에 할당하고, 학습 데이터세트의 색인숫자를 인자 y에 할당하면 앞에서 말한 여집합에 해당하는 원소를 얻을 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
df_test = df[setdiff(x = 1:nrow(df), y = idx_train), ]
head(df_test)
##    carat       cut color clarity depth table price    x    y    z
## 1   0.23     Ideal     E     SI2  61.5    55   326 3.95 3.98 2.43
## 4   0.29   Premium     I     VS2  62.4    58   334 4.20 4.23 2.63
## 13  0.22   Premium     F     SI1  60.4    61   342 3.88 3.84 2.33
## 14  0.31     Ideal     J     SI2  62.2    54   344 4.35 4.37 2.71
## 15  0.20   Premium     E     SI2  60.2    62   345 3.79 3.75 2.27
## 20  0.30 Very Good     J     SI1  62.7    59   351 4.21 4.27 2.66

nrow(df_test)
## [1] 13940

nrow(df) == (nrow(df_train) + nrow(df_test)) # 데이터 세트 개수 검증
## [1] TRUE

하지만 R에는 마이너스 부호를 활용하여 setdiff() 함수와 거의 비슷한 기능을 구현할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
df_test = df[-idx_train, ]
head(df_test)
##    carat       cut color clarity depth table price    x    y    z
## 1   0.23     Ideal     E     SI2  61.5    55   326 3.95 3.98 2.43
## 4   0.29   Premium     I     VS2  62.4    58   334 4.20 4.23 2.63
## 13  0.22   Premium     F     SI1  60.4    61   342 3.88 3.84 2.33
## 14  0.31     Ideal     J     SI2  62.2    54   344 4.35 4.37 2.71
## 15  0.20   Premium     E     SI2  60.2    62   345 3.79 3.75 2.27
## 20  0.30 Very Good     J     SI1  62.7    59   351 4.21 4.27 2.66

nrow(df_test)
## [1] 13940

nrow(df) == (nrow(df_train) + nrow(df_test)) # 데이터 세트 개수 검증
## [1] TRUE

다음은 사전에 지정한 정수가 아니라 비율 계산으로 데이터세트를 분리하여 70%의 학습 데이터세트를 분리하는 코드는 다음과 같다.

1
2
3
4
5
6
set.seed(123)
proportion = 0.7
idx_train = sample(1:nrow(df), size = round(proportion * nrow(df)))
df_train = df[idx_train, ]
nrow(df_train)
## [1] 37758

실제로 사용하는 코드는 더 간단하겠지만 일부러 코드를 좀 더 풀어보면 앞의 코드와 같다. 비율에 해당하는 값을 proportion 객체에 할당하면 되겠고, round() 함수가 기본을 반올림 하여 1의 자리까지 산출해주기 때문에 앞의 코드와 같이 사용하였다. 물론 round() 함수 이외에도 floor() 같은 수를 어림하는 함수를 사용해도 괜찮다.

패키지 사용

dplyr

dplyr 패키지는 앞에서 구현해본 표본추출을 보다 간단하게 할 수 있게 지원하는 함수가 있다. sample_n() 함수는 지정한 개수만큼, sample_frac() 함수는 지정한 비율만큼 추출해주며 sample_frac() 함수를 사용한 예제는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
library("dplyr")
df_train = sample_frac(df, size = 0.7)
head(df_train)
##   carat       cut color clarity depth table price    x    y    z
## 1  0.61   Premium     D     SI2  60.8    57  1308 5.48 5.40 3.31
## 2  1.01     Ideal     G     SI2  61.6    54  4560 6.40 6.45 3.96
## 3  1.39     Ideal     J     VS2  60.3    57  6366 7.26 7.24 4.37
## 4  0.30   Premium     J     VS1  62.6    60   506 4.28 4.22 2.66
## 5  0.70 Very Good     F    VVS2  60.5    60  3205 5.70 5.73 3.46
## 6  1.52      Fair     H     SI2  64.9    58  6129 7.16 7.13 4.64

nrow(df_train)
## [1] 37758

dplyr 패키지를 통한 샘플링의 경우 숙지해야 할 사항이 있다. 보통 표본 추출은 확률적 표본 추출을 하기 때문에 임의의 행(random row)를 추출하지만 예전 버전(2021년 이전)의 dplyr 의 함수는 지정된 숫자 또는 비율 만큼 첫 행 부터 뽑아온다. 그렇기에 별도의 목적이 있지 않은 이상 표본이 편향될 가능성이 확률적 표본 추출 보다 높기 때문에 조심하도록 하자. 혹시 불안하다면 install.packages() 함수로 dplyr 패키지를 업데이트 한 다음에 사용하는 것도 방법이다.

caTools

머신러닝 패키지 중 하나인 caTools의 예제는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
library("caTools")
set.seed(123)
idx_train = sample.split(Y = df$carat, SplitRatio = 0.7)
df_train = df[idx_train, ]
head(df_train)
##    carat       cut color clarity depth table price    x    y    z
## 1   0.23     Ideal     E     SI2  61.5    55   326 3.95 3.98 2.43
## 5   0.31      Good     J     SI2  63.3    58   335 4.34 4.35 2.75
## 6   0.24 Very Good     J    VVS2  62.8    57   336 3.94 3.96 2.48
## 8   0.26 Very Good     H     SI1  61.9    55   337 4.07 4.11 2.53
## 9   0.22      Fair     E     VS2  65.1    61   337 3.87 3.78 2.49
## 10  0.23 Very Good     H     VS1  59.4    61   338 4.00 4.05 2.39

nrow(df_train)
## [1] 37760

최적의 비율

그런거 없다. 학습:평가 비율을 7:3으로 하거나 8:2로 하는 것을 영어권에서는 rule of thumbs 로 친다. 즉, 저렇게 하면 따봉 하나 준다는 얘기이다. 명확한 기준은 아닐지언정 적당히 저정도 하면 끄덕끄덕 하면서 넘어가는 숫자이다. 혹시나 연도로 구분되어 있는 경우에는 5개년도 데이터가 있다면, 최초 4년은 학습으로 사용하고 마지막 1년치 데이터를 평가로 사용하기도 한다.

하지만 표본추출은 확률적 표본추출 중에서 단순 임의 추출을 사용한다고 했을 때, 독립변수의 이상치만 잔뜩 뽑혀서 test 세트에 들어간다던지 명목형 변수의 특정 class만 한 변수에 쏠릴 수 있다. 이 문제를 해결하려면 군집 또는 층화 표본추출을 사용해야 한다. 표본추출 관련해서 좀 더 전문적으로 하고싶다면 표본조사론 또는 sampling 패키지를 참고하도록 하자.

# , , , , , ,
327142-eng.png
[R을 R려줘] R 데이터 시각화
326871-eng.png
[R을 R려줘] R 기초다지기

Inflearn에서 인강을 평생 소장하세요!

R) 기본 1차원 벡터 - 생성
R) 객체 용량 확인

카테고리

Your browser is out-of-date!

Update your browser to view this website correctly. Update my browser now

×